Machine Learning (ML) is a branch of Artificial Intelligence (AI) that enables computer systems to learn from data without being explicitly programmed. The goal of ML is to develop algorithms and models that can automatically identify patterns and make predictions or decisions from data.
In general, there are three main types of ML: supervised learning, unsupervised learning, and reinforcement learning.
Supervised learning is the process of training a model on a labeled dataset, where the desired output (label) is provided for each input. Common tasks include classification and regression. Unsupervised learning is the process of training a model on an unlabeled dataset, where the goal is to find patterns or structure in the data. Common tasks include clustering and dimensionality reduction. Reinforcement learning is a type of ML where an agent learns to make decisions by interacting with an environment and receiving feedback in the form of rewards or penalties. There are various techniques and algorithms used in ML, such as:
Decision Trees: A decision tree is a flowchart-like tree structure, where an internal node represents a feature(or attribute), the branch represents a decision rule, and each leaf node represents the outcome. Support Vector Machines (SVMs): A supervised learning algorithm that can be used for classification or regression tasks. Neural Networks: A set of algorithms, modeled loosely after the human brain, that are designed to recognize patterns. Bayesian Networks: A probabilistic graphical model that represents a set of variables and their conditional dependencies via a directed acyclic graph. Genetic Algorithm: A search heuristic that is inspired by the process of natural selection. To get started with ML, it's important to have a strong understanding of linear algebra, calculus, and probability. Additionally, many popular platforms and libraries, such as TensorFlow, PyTorch, and scikit-learn, make it easier to implement ML algorithms and models.
Understanding the problem: This includes identifying the inputs, outputs, and constraints of the problem. Choosing a model: This includes selecting a model architecture and hyperparameters that are appropriate for the problem and dataset. Choosing a loss function: This includes selecting a function that measures the difference between the model's predictions and the true outputs. Choosing an optimizer: This includes selecting an algorithm that updates the model's parameters to minimize the loss function. Choosing a metric: This includes selecting a function that measures the performance of the model on a held-out dataset. Choosing a dataset: This includes selecting a dataset that is appropriate for the problem and the model. Machine learning is an iterative process, and the model is typically trained multiple times using different combinations of hyperparameters, architectures, and datasets. The goal is to find the best set of parameters that result in the best performance on the held-out dataset.
Overfitting and underfitting are common issues that arise during the learning process. Overfitting occurs when the model is too complex and memorizes the training data instead of generalizing to new data. Underfitting occurs when the model is too simple and is not able to capture the underlying patterns in the data.
To prevent overfitting, techniques such as regularization and early stopping can be used. To prevent underfitting, techniques such as increasing the model complexity or increasing the size of the dataset can be used.
Please note that the above information is just a brief overview of the topic, and you should consult your course materials and instructors for a more comprehensive understanding of learning in the context of machine learning techniques.
Supervised Learning is a type of machine learning in which a model or algorithm is trained on a labeled dataset, and then used to make predictions or take actions in new, unseen situations. Here are some notes on Supervised Learning with reference to Machine Learning Techniques:
Definition: Supervised learning is a process where a model learns from labeled training data, which includes input-output pairs, and makes predictions on unseen data. The goal is to learn a function that maps inputs to outputs.
Types of Supervised Learning:
Classification: The goal is to predict a categorical label (e.g. spam or not spam) based on the input data. Common algorithms include logistic regression, decision trees, and support vector machines.
Regression: The goal is to predict a continuous value (e.g. price of a stock) based on the input data. Common algorithms include linear regression and polynomial regression.
Training and Testing: In supervised learning, the training data is used to train the model and the testing data is used to evaluate its performance. The testing data should be independent of the training data to avoid overfitting.
Evaluation Metrics: The performance of a supervised learning model is typically evaluated using metrics such as accuracy, precision, recall, and F1 score (for classification) or mean squared error (for regression).
Applications: Supervised learning algorithms are widely used in a variety of applications, including natural language processing, computer vision, speech recognition, and bioinformatics.
Limitations: Supervised learning algorithms can be limited by the quality and representativeness of the training data, and may not be able to generalize well to new, unseen data. Additionally, they require labeled data to train the model which is not always available and it can be time-consuming and expensive to label data.
Supervised Learning is a fundamental concept in the field of Machine Learning Techniques, and is widely used in a variety of applications. A comprehensive understanding of Supervised Learning includes not only the basic concepts and definitions but also the underlying algorithms, techniques, and best practices used to implement it.
Definition: Supervised learning is a process where a model learns from labeled training data, which includes input-output pairs, and makes predictions on unseen data. The goal is to learn a function that maps inputs to outputs. The model is trained on a labeled dataset, where each example has an input and an associated output. Once the model is trained, it can be used to make predictions on new, unseen data.
Types of Supervised Learning: There are two main types of supervised learning: classification and regression.
Classification: The goal is to predict a categorical label (e.g. spam or not spam) based on the input data. Common algorithms for classification include logistic regression, decision trees, k-nearest neighbors, and support vector machines. Regression: The goal is to predict a continuous value (e.g. price of a stock) based on the input data. Common algorithms for regression include linear regression, polynomial regression, and decision tree regression. Training and Testing: In supervised learning, the training data is used to train the model and the testing data is used to evaluate its performance. The testing data should be independent of the training data to avoid overfitting. A common practice is to split the data into a training set and a test set, where the model is trained on the training set and evaluated on the test set.
Evaluation Metrics: The performance of a supervised learning model is typically evaluated using metrics such as accuracy, precision, recall, and F1 score (for classification) or mean squared error (for regression). These metrics allow us to quantitatively measure how well the model is performing and compare the performance of different models. Other evaluation metrics like ROC-AUC, Log-loss, etc can also be used depending on the type of problem.
Feature Selection and Engineering: Supervised learning models are sensitive to the features of the input data, and the performance of the model can be greatly improved by selecting relevant features and transforming the input data in a way that is more informative. Feature selection techniques like Recursive Feature Elimination, Correlation-based Feature Selection, etc can be used to select the most relevant features and feature engineering techniques like PCA, LDA, etc can be used to transform the input data.
Hyperparameter tuning: Supervised learning models often have a number of parameters that must be set before training. These are called hyperparameters and their optimal values are determined by tuning them on a validation set. Common techniques for hyperparameter tuning include grid search, random search and Bayesian optimization.
Bias-variance trade-off: Supervised learning models can suffer from either high bias or high variance, and it is important to understand the bias-variance trade-off to select the best model. High bias models are simple and tend to underfit the data, while high variance models are complex and tend to overfit the data. Techniques like k-fold cross-validation, regularization, and early stopping can be used to balance bias and variance and improve the performance of the model.
Ensemble Methods: Ensemble methods are used to combine the predictions of multiple models to improve the overall performance. Common ensemble methods include bagging, boosting and stacking. Bagging method like Random Forest and Boosting method like Adaboost are widely used in supervised learning.
Applications: Supervised learning algorithms are widely used in a variety of applications, including natural language processing, computer vision, speech recognition, bioinformatics, financial forecasting, and customer churn prediction.
Limitations: Supervised learning algorithms can be limited by the quality and representativeness of the training data, and may not be able to generalize well to new, unseen data. Additionally, they require labeled data to train the model which is not always available and it can be time-consuming and expensive to label data.
In conclusion, a comprehensive understanding of Supervised Learning with reference to Machine Learning Techniques requires knowledge of the basic concepts, types of learning, underlying algorithms, techniques, and best practices used to implement it, as well as an understanding of its limitations and applications. It's important to keep in mind that this is an active area of research and new techniques and algorithms are being developed all the time.
Unsupervised Learning is a type of machine learning in which a model or algorithm is trained on an unlabeled dataset, and then used to identify patterns or structure in the data. Here are some notes on Unsupervised Learning with reference to Machine Learning Techniques:
Definition: Unsupervised learning is a process where a model learns from unlabeled data, and tries to identify patterns or structure in the data. The goal is to discover hidden structure in the data, rather than making predictions.
Types of Unsupervised Learning: There are several types of unsupervised learning, including clustering, dimensionality reduction, and anomaly detection.
Clustering: The goal is to group similar data points together. Common algorithms include k-means, hierarchical clustering, and DBSCAN.
Dimensionality Reduction: The goal is to reduce the number of features in the data while preserving as much information as possible. Common algorithms include PCA, LLE, and t-SNE.
Anomaly Detection: The goal is to identify data points that do not conform to the general pattern of the data. Common algorithms include One-class SVM and Isolation Forest.
Evaluation Metrics: Evaluating the performance of unsupervised learning models can be challenging, as there is no clear criterion for success. Common metrics include silhouette score, Davies-Bouldin index, and Calinski-Harabasz index for Clustering.
Applications: Unsupervised learning algorithms are widely used in a variety of applications, including image compression, market segmentation, and anomaly detection in financial and healthcare industries.
Limitations: Unsupervised learning algorithms can be limited by the quality and representativeness of the data, and may not be able to identify all the underlying patterns or structure in the data. Additionally, it may not be clear what the output of the model represents and how to interpret the results.
In conclusion, a comprehensive understanding of Unsupervised Learning with reference to Machine Learning Techniques requires knowledge of the basic concepts, types of learning, underlying algorithms, techniques, and best practices used to implement it, as well as an understanding of its limitations and applications. It's important to keep in mind that this is an active area of research and new techniques and algorithms are being developed all the time.
Reinforcement Learning is a type of machine learning in which a model or algorithm is trained on an unlabeled dataset, and then used to make predictions or take actions in new, unseen situations. Here are some notes on Reinforcement Learning with reference to Machine Learning Techniques:
Definition: Reinforcement learning is a process where a model learns from feedback from the environment, in the form of rewards or penalties, and makes predictions or takes actions on unseen data. The goal is to learn a policy that maximizes the cumulative reward over time.
Types of Reinforcement Learning: There are two main types of reinforcement learning: policy-based and value-based.
Policy-Based: The goal is to learn a mapping between states and actions, called a policy, which determines the action that should be taken in each state. Common algorithms include policy gradient and Q-learning.
Value-Based: The goal is to learn a mapping between states and values, called a value function, which estimates the value of being in each state. Common algorithms include policy iteration and value iteration.
Training and Testing: In reinforcement learning, the training data is used to train the model and the testing data is used to evaluate its performance. The testing data should be independent of the training data to avoid overfitting.
Evaluation Metrics: The performance of a reinforcement learning model is typically evaluated using metrics such as cumulative reward and average reward per episode.
Applications:
Limitations:
A well-defined learning problem is a crucial aspect of machine learning. It is important to define the problem clearly before attempting to solve it with machine learning techniques. A well-defined learning problem includes a clear statement of the task, input data, output data and performance measure. Here are some notes on well-defined learning problems with reference to Machine Learning Techniques:
Task: The task should be defined clearly and in a specific way. For example, "predicting the price of a stock" is a more specific task than "predicting the stock market."
Input Data: The input data should be clearly defined and understood. It should include the type of data, format, and any preprocessing that needs to be done.
Output Data: The output data should be clearly defined and understood. It should include the type of data, format, and any post-processing that needs to be done.
Performance Measure: The performance measure should be clearly defined and understood. It should include the evaluation metric that will be used to measure the performance of the model.
In Machine Learning Techniques, a well-defined learning problem is a problem where the input, output, and desired behavior of the model are clearly specified. A well-defined learning problem is essential for the successful implementation of a machine learning model. Here are some notes on well-defined learning problems with reference to Machine Learning Techniques:
Definition: A well-defined learning problem is a problem where the input, output, and desired behavior of the model are clearly specified. This includes the type of input, the type of output, and the performance criteria for the model.
Examples:
A supervised learning problem where the input is an image and the output is a label indicating whether the image contains a dog or a cat. A supervised learning problem where the input is a customer's historical data and the output is a prediction of whether the customer will churn. A unsupervised learning problem where the input is a set of market transactions and the goal is to find patterns or clusters in the data. Mnemonics: To remember the importance of well-defined learning problems, one can use the mnemonic "CLEAR"
C stands for "clearly defined inputs and outputs" L stands for "learning goal is defined" E stands for "evaluation metric is defined" A stands for "algorithms are chosen based on the problem" R stands for "real-world scenario" Real-world Scenario: In real-world scenarios, a well-defined learning problem is crucial for the successful implementation of machine learning models. For example, in the healthcare industry, a well-defined learning problem would be to predict the likelihood of a patient developing a certain disease based on their medical history and test results. The input would be the patient's medical history and test results, the output would be a probability of the patient developing the disease, and the performance criteria would be the accuracy of the predictions. With a well-defined learning problem, appropriate algorithms can be chosen, and the model can be evaluated using the chosen metric.
In conclusion, a well-defined learning problem is essential for the successful implementation of machine learning models. It allows for the clear specification of inputs, outputs, and desired behavior, which in turn enables the selection of appropriate algorithms and the evaluation of model performance.
According to Arthur Samuel “Machine Learning enables a Machine to Automatically learn from Data, Improve performance from an Experience and predict things without explicitly programmed.”
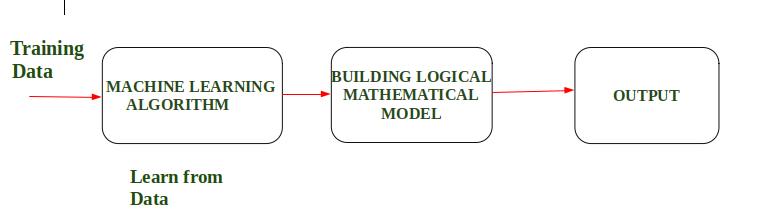
In Simple Words, When we fed the Training Data to Machine Learning Algorithm, this algorithm will produce a mathematical model and with the help of the mathematical model, the machine will make a prediction and take a decision without being explicitly programmed. Also, during training data, the more machine will work with it the more it will get experience and the more efficient result is produced.

Example : In Driverless Car, the training data is fed to Algorithm like how to Drive Car in Highway, Busy and Narrow Street with factors like speed limit, parking, stop at signal etc. After that, a Logical and Mathematical model is created on the basis of that and after that, the car will work according to the logical model. Also, the more data the data is fed the more efficient output is produced.
Designing a Learning System in Machine Learning :
According to Tom Mitchell, “A computer program is said to be learning from experience (E), with respect to some task (T). Thus, the performance measure (P) is the performance at task T, which is measured by P, and it improves with experience E.”
Example: In Spam E-Mail detection,
Task, T: To classify mails into Spam or Not Spam. Performance measure, P: Total percent of mails being correctly classified as being “Spam” or “Not Spam”. Experience, E: Set of Mails with label “Spam” Steps for Designing Learning System are:
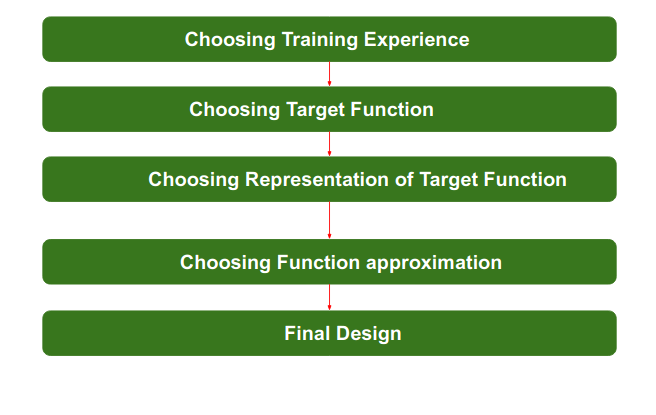
Step 1) Choosing the Training Experience: The very important and first task is to choose the training data or training experience which will be fed to the Machine Learning Algorithm. It is important to note that the data or experience that we fed to the algorithm must have a significant impact on the Success or Failure of the Model. So Training data or experience should be chosen wisely.
Below are the attributes which will impact on Success and Failure of Data:
The training experience will be able to provide direct or indirect feedback regarding choices. For example: While Playing chess the training data will provide feedback to itself like instead of this move if this is chosen the chances of success increases. Second important attribute is the degree to which the learner will control the sequences of training examples. For example: when training data is fed to the machine then at that time accuracy is very less but when it gains experience while playing again and again with itself or opponent the machine algorithm will get feedback and control the chess game accordingly. Third important attribute is how it will represent the distribution of examples over which performance will be measured. For example, a Machine learning algorithm will get experience while going through a number of different cases and different examples. Thus, Machine Learning Algorithm will get more and more experience by passing through more and more examples and hence its performance will increase. Step 2- Choosing target function: The next important step is choosing the target function. It means according to the knowledge fed to the algorithm the machine learning will choose NextMove function which will describe what type of legal moves should be taken. For example : While playing chess with the opponent, when opponent will play then the machine learning algorithm will decide what be the number of possible legal moves taken in order to get success.
Step 3- Choosing Representation for Target function: When the machine algorithm will know all the possible legal moves the next step is to choose the optimized move using any representation i.e. using linear Equations, Hierarchical Graph Representation, Tabular form etc. The NextMove function will move the Target move like out of these move which will provide more success rate. For Example : while playing chess machine have 4 possible moves, so the machine will choose that optimized move which will provide success to it.
Step 4- Choosing Function Approximation Algorithm: An optimized move cannot be chosen just with the training data. The training data had to go through with set of example and through these examples the training data will approximates which steps are chosen and after that machine will provide feedback on it. For Example : When a training data of Playing chess is fed to algorithm so at that time it is not machine algorithm will fail or get success and again from that failure or success it will measure while next move what step should be chosen and what is its success rate.
Step 5- Final Design: The final design is created at last when system goes from number of examples , failures and success , correct and incorrect decision and what will be the next step etc. Example: DeepBlue is an intelligent computer which is ML-based won chess game against the chess expert Garry Kasparov, and it became the first computer which had beaten a human chess expert.
It’s all well and good to ask if androids dream of electric sheep, but science fact has evolved to a point where it’s beginning to coincide with science fiction. No, we don’t have autonomous androids struggling with existential crises — yet — but we are getting ever closer to what people tend to call “artificial intelligence.”
Machine Learning is a sub-set of artificial intelligence where computer algorithms are used to autonomously learn from data and information. In machine learning computers don’t have to be explicitly programmed but can change and improve their algorithms by themselves.
Today, machine learning algorithms enable computers to communicate with humans, autonomously drive cars, write and publish sport match reports, and find terrorist suspects. I firmly believe machine learning will severely impact most industries and the jobs within them, which is why every manager should have at least some grasp of what machine learning is and how it is evolving.
In this post I offer a quick trip through time to examine the origins of machine learning as well as the most recent milestones.
1950 — Alan Turing creates the “Turing Test” to determine if a computer has real intelligence. To pass the test, a computer must be able to fool a human into believing it is also human.
1952 — Arthur Samuel wrote the first computer learning program. The program was the game of checkers, and the IBM computer improved at the game the more it played, studying which moves made up winning strategies and incorporating those moves into its program.
1957 — Frank Rosenblatt designed the first neural network for computers (the perceptron), which simulate the thought processes of the human brain.
1967 — The “nearest neighbor” algorithm was written, allowing computers to begin using very basic pattern recognition. This could be used to map a route for traveling salesmen, starting at a random city but ensuring they visit all cities during a short tour.
1979 — Students at Stanford University invent the “Stanford Cart” which can navigate obstacles in a room on its own.
1981 — Gerald Dejong introduces the concept of Explanation Based Learning (EBL), in which a computer analyses training data and creates a general rule it can follow by discarding unimportant data.
Machine Learning (source: Shutterstock) Machine Learning (source: Shutterstock) 1985 — Terry Sejnowski invents NetTalk, which learns to pronounce words the same way a baby does.
1990s — Work on machine learning shifts from a knowledge-driven approach to a data-driven approach. Scientists begin creating programs for computers to analyze large amounts of data and draw conclusions — or “learn” — from the results.
1997 — IBM’s Deep Blue beats the world champion at chess.
2006 — Geoffrey Hinton coins the term “deep learning” to explain new algorithms that let computers “see” and distinguish objects and text in images and videos.
2010 — The Microsoft Kinect can track 20 human features at a rate of 30 times per second, allowing people to interact with the computer via movements and gestures.
2011 — IBM’s Watson beats its human competitors at Jeopardy.
2011 — Google Brain is developed, and its deep neural network can learn to discover and categorize objects much the way a cat does.
2012 – Google’s X Lab develops a machine learning algorithm that is able to autonomously browse YouTube videos to identify the videos that contain cats.
2014 – Facebook develops DeepFace, a software algorithm that is able to recognize or verify individuals on photos to the same level as humans can.
2015 – Amazon launches its own machine learning platform.
2015 – Microsoft creates the Distributed Machine Learning Toolkit, which enables the efficient distribution of machine learning problems across multiple computers.
2015 – Over 3,000 AI and Robotics researchers, endorsed by Stephen Hawking, Elon Musk and Steve Wozniak (among many others), sign an open letter warning of the danger of autonomous weapons which select and engage targets without human intervention.
2016 – Google’s artificial intelligence algorithm beats a professional player at the Chinese board game Go, which is considered the world’s most complex board game and is many times harder than chess. The AlphaGo algorithm developed by Google DeepMind managed to win five games out of five in the Go competition.
So are we drawing closer to artificial intelligence? Some scientists believe that’s actually the wrong question.
They believe a computer will never “think” in the way that a human brain does, and that comparing the computational analysis and algorithms of a computer to the machinations of the human mind is like comparing apples and oranges.
Regardless, computers’ abilities to see, understand, and interact with the world around them is growing at a remarkable rate. And as the quantities of data we produce continue to grow exponentially, so will our computers’ ability to process and analyze — and learn from — that data grow and expand.
With the constant advancements in artificial intelligence, the field has become too big to specialize in all together. There are countless problems that we can solve with countless methods. Knowledge of an experienced AI researcher specialized in one field may mostly be useless for another field. Understanding the nature of different machine learning problems is very important. Even though the list of machine learning problems is very long and impossible to explain in a single post, we can group these problems into four different learning approaches:
Supervised Learning; Unsupervised Learning; Semi-supervised Learning; and Reinforcement Learning. Before we dive into each of these approaches, let’s start with what machine learning is:
What is Machine Learning? The term “Machine Learning” was first coined in 1959 by Arthur Samuel, an IBM scientist and pioneer in computer gaming and artificial intelligence. Machine learning is considered a sub-discipline under the field of artificial intelligence. It aims to automatically improve the performance of the computer algorithms designed for particular tasks using experience. In a machine learning study, the experience is derived from the training data, which may be defined as the sample data collected on previously recorded observations or live feedbacks. Through this experience, machine learning algorithms can learn and build mathematical models to make predictions and decisions.
The learning process starts by feeding training data (e.g., examples, direct experience, basic instructions) into the model. By using these data, models can find valuable patterns in the data very quickly. These patterns are -then- used to make predictions and decisions on relevant events. The learning may continue even after deployment if the developer builds a suitable machine learning system which allows continuous training.
Four Machine Learning Approaches Top machine learning approaches are categorized depending on the nature of their feedback mechanism for learning. Most of the machine learning problems may be addressed by adopting one of these approaches. Yet, we may still encounter complex machine learning solutions that do not fit into one of these approaches.
This categorization is essential because it will help you quickly uncover the nature of a problem you may encounter in the future, analyze your resources, and develop a suitable solution.
Let’s start with the supervised learning approach.
Supervised Learning Supervised learning is the machine learning task of learning a function that maps an input to an output based on example input-output pairs. It infers a function from labeled training data consisting of a set of training examples.
The supervised learning approach can be adopted when a dataset contains the records of the response variable values (or labels). Depending on the context, this data with labels is usually referred to as “labeled data” and “training data.”
Example 1: When we try to predict a person’s height using his weight, age, and gender, we need the training data that contains people’s weight, age, gender info along with their real heights. This data allows the machine learning algorithm to discover the relationship between height and the other variables. Then, using this knowledge, the model can predict the height of a given person.
Example 2: We can mark e-mails as ‘spam’ or ‘not-spam’ based on the differentiating features of the previously seen spam and not-spam e-mails, such as the lengths of the e-mails and use of particular keywords in the e-mails. Learning from training data continues until the machine learning model achieves a high level of accuracy on the training data.
There are two main supervised learning problems: (i) Classification Problems and (ii) Regression Problems.
Classification Problem In classification problems, the models learn to classify an observation based on their variable values. During the learning process, the model is exposed to a lot of observations with their labels. For example, after seeing thousands of customers with their shopping habits and gender information, a model may successfully predict the gender of a new customer based on his/her shopping habits. Binary classification is the term used for grouping under two labels, such as male and female. Another binary classification example might be predicting whether the animal in a picture is a ‘cat’ or ‘not cat,’ as shown in Figure 2–4.
On the other hand, multilabel classification is used when there are more than two labels. Identifying and predicting handwritten letters and numbers on an image would be an example of multilabel classification.
Regression Problems In regression problems, the goal is to calculate a value by taking advantage of the relationship between the other variables (i.e., independent variables, explanatory variables, or features) and the target variable (i.e., dependent variable, response variable, or label). The strength of the relationship between our target variable and the other variables is a critical determinant of the prediction value. Predicting how much a customer would spend based on its historical data is a regression problem.
Unsupervised Learning Unsupervised learning is a type of machine learning that looks for previously undetected patterns in a data set with no pre-existing labels and with a minimum of human supervision.
Unsupervised learning is a learning approach used in ML algorithms to draw inferences from datasets, which do not contain labels.
There are two main unsupervised learning problems: (i) Clustering and (ii) Dimensionality Reduction.
Clustering Unsupervised learning is mainly used in clustering analysis.
Clustering analysis is a grouping effort in which the members of a group (i.e., a cluster) are more similar to each other than the members of the other clusters.
There are many different clustering methods available. They usually utilize a type of similarity measure based on selected metrics such as Euclidean or probabilistic distance. Bioinformatic sequence analysis, genetic clustering, pattern mining, and object recognition are some of the clustering problems that may be tackled with the unsupervised learning approach.
Dimensionality Reduction Another use case of unsupervised learning is dimensionality reduction. Dimensionality is equivalent to the number of features used in a dataset. In some datasets, you may find hundreds of potential features stored in individual columns. In most of these datasets, several of these columns are highly correlated. Therefore, we should either select the best ones, i.e., feature selection, or extract new features combining the existing ones, i.e., feature extraction. This is where unsupervised learning comes into play. Dimensionality reduction methods help us create neater and cleaner models that are free of noise and unnecessary features.
Semi-Supervised Learning Semi-supervised learning is a machine learning approach that combines the characteristics of supervised learning and unsupervised learning. A semi-supervised learning approach is particularly useful when we have a small amount of labeled data with a large amount of unlabeled data available for training. Supervised learning characteristics help take advantage of the small amount of label data. In contrast, unsupervised learning characteristics are useful to take advantage of a large amount of unlabeled data.
Semi-supervised learning is an approach to machine learning that combines a small amount of labeled data with a large amount of unlabeled data during training.
Well, you might think that if there are useful real-life applications for semi-supervised learning. Although supervised learning is a powerful learning approach, labeling data -to be used in supervised learning- is a costly and time-consuming process. On the other hand, a sizeable data volume can also be beneficial even though they are not labeled. So, in real life, semi-supervised learning may shine out as the most suitable and the most fruitful ML approach if done correctly.
In semi-supervised learning, we usually start by clustering the unlabeled data. Then, we use the labeled data to label the clustered unlabeled data. Finally, a significant amount of now-labeled data is used to train machine learning models. Semi-supervised learning models can be very powerful since they can take advantage of a high volume of data.
Semi-supervised learning models are usually a combination of transformed and adjusted versions of the existing machine learning algorithms used in supervised and unsupervised learning. This approach is successfully used in areas like speech analysis, content classification, and protein sequence classification. The similarity of these fields is that they offer abundant unlabeled data and only a small amount of labeled data.
Reinforcement Learning Reinforcement learning is one of the primary approaches to machine learning concerned with finding optimal agent actions that maximize the reward within a particular environment. The agent learns to perfect its actions to gain the highest possible cumulative reward.
Reinforcement learning (RL) is an area of machine learning concerned with how software agents ought to take actions in an environment in order to maximize the notion of cumulative reward.
There are four main elements in reinforcement learning:
Agent: The trainable program which exercises the tasks assigned to it Environment: The real or virtual universe where the agent completes its tasks. Action: A move of the agent which results in a change of status in the environment Reward: A negative or positive remuneration based on the action. Reinforcement learning may be used in both the real world as well as in the virtual world:
Example 1: You may create an evolving ad placement system deciding how many ads to place on a website based on the ad revenue generated in different setups. The ad placement system would be an excellent example of real-world applications.
Example 2: On the other hand, you can train an agent in a video game with reinforcement learning to compete against other players, usually referred to as bots.
Example 3: Finally, virtual and real robots training in terms of their movements are done with the reinforcement learning approach.
Some of the popular reinforcement learning models may be listed as follows:
Q-Learning, State-Action-Reward-State-Action (SARSA), Deep Q Network (DQN), Deep Deterministic Policy Gradient (DDPG), One of the disadvantages of the popular deep learning frameworks is that they lack comprehensive module support for reinforcement learning, and TensorFlow and PyTorch are no exception. Deep reinforcement learning can only be done with extension libraries built on top of existing deep learning libraries such as Keras-RL, TF.Agents, and Tensorforce or dedicated reinforcement learning libraries such as Open AI Baselines and Stable Baselines.
Now that we covered all four approaches, here is a summary visual to make basic comparison among different ML approaches:
Final Notes The field of AI is expanding very quickly and becoming a major research field. As the field expands, sub-fields and sub-subfields of AI have started to appear. Although we cannot master the entire field, we can at least be informed about the major learning approach.
The purpose of this post was to make you acquainted with these four machine learning approaches. In the upcoming post, we will cover other AI essentials.
Artificial neural networks (ANNs), usually simply called neural networks (NNs) or neural nets, are computing systems inspired by the biological neural networks that constitute animal brains.
An ANN is based on a collection of connected units or nodes called artificial neurons, which loosely model the neurons in a biological brain. Each connection, like the synapses in a biological brain, can transmit a signal to other neurons. An artificial neuron receives signals then processes them and can signal neurons connected to it. The "signal" at a connection is a real number, and the output of each neuron is computed by some non-linear function of the sum of its inputs. The connections are called edges. Neurons and edges typically have a weight that adjusts as learning proceeds. The weight increases or decreases the strength of the signal at a connection. Neurons may have a threshold such that a signal is sent only if the aggregate signal crosses that threshold.
Typically, neurons are aggregated into layers. Different layers may perform different transformations on their inputs. Signals travel from the first layer (the input layer), to the last layer (the output layer), possibly after traversing the layers multiple times.
The original goal of neural networks was to model the brain, but they have also been used for statistical modeling and data mining. Neural networks are used in applications such as speech recognition, image recognition, medical diagnosis, and natural language processing. Neural networks are also used in reinforcement learning, a form of machine learning that allows software agents to automatically determine the ideal behavior within a specific context in order to maximize its performance.
Artificial Neuron is a mathematical model of a biological neuron. It is a mathematical function that takes a set of inputs, performs a calculation on them, and produces a single output. The output of the artificial neuron is a function of the inputs and the weights associated with the inputs. The artificial neuron is a basic unit of a neural network. It is a mathematical function that takes a set of inputs, performs a calculation on them, and produces a single output. The output of the artificial neuron is a function of the inputs and the weights associated with the inputs. The artificial neuron is a basic unit of a neural network.
Clustering is the task of grouping a set of objects in such a way that objects in the same group (called a cluster) are more similar (in some sense or another) to each other than to those in other groups (clusters). Clustering is a main task of exploratory data mining, and a common technique for statistical data analysis, used in many fields, including machine learning, pattern recognition, image analysis, information retrieval, bioinformatics, data compression, and computer graphics.
Clustering is a method of unsupervised learning, which is used when you have unlabeled data (i.e., data without defined categories or groups). The goal of clustering is to identify the inherent groupings in the data, such as grouping customers by purchasing behavior. Clustering is also used for exploratory data analysis to find hidden patterns or grouping in data.
In the field of machine learning, clustering is one of the most popular unsupervised learning methods. Clustering is used for exploratory data analysis to find hidden patterns or grouping in data. Clustering is also used for customer segmentation, recommender systems, image segmentation, semi-supervised learning, and dimensionality reduction.
The main goal of clustering is to group the data into distinct groups, such that the data points in the same group are similar to each other and dissimilar to the data points in other groups. There are several clustering algorithms, such as K-means, hierarchical clustering, DBSCAN, and Gaussian mixture models. The K-means algorithm is one of the most popular clustering algorithms and is used for a wide range of applications.
Types of clustering
Here we are discussing mainly popular Clustering algorithms that are widely used in machine learning:
K-Means algorithm: The k-means algorithm is one of the most popular clustering algorithms. It classifies the dataset by dividing the samples into different clusters of equal variances. The number of clusters must be specified in this algorithm. It is fast with fewer computations required, with the linear complexity of O(n). Mean-shift algorithm: Mean-shift algorithm tries to find the dense areas in the smooth density of data points. It is an example of a centroid-based model, that works on updating the candidates for centroid to be the center of the points within a given region. DBSCAN Algorithm: It stands for Density-Based Spatial Clustering of Applications with Noise. It is an example of a density-based model similar to the mean-shift, but with some remarkable advantages. In this algorithm, the areas of high density are separated by the areas of low density. Because of this, the clusters can be found in any arbitrary shape. Expectation-Maximization Clustering using GMM: This algorithm can be used as an alternative for the k-means algorithm or for those cases where K-means can be failed. In GMM, it is assumed that the data points are Gaussian distributed. Agglomerative Hierarchical algorithm: The Agglomerative hierarchical algorithm performs the bottom-up hierarchical clustering. In this, each data point is treated as a single cluster at the outset and then successively merged. The cluster hierarchy can be represented as a tree-structure. Affinity Propagation: It is different from other clustering algorithms as it does not require to specify the number of clusters. In this, each data point sends a message between the pair of data points until convergence. It has O(N2T) time complexity, which is the main drawback of this algorithm.
Applications of Clustering
Below are some commonly known applications of clustering technique in Machine Learning:
In Identification of Cancer Cells: The clustering algorithms are widely used for the identification of cancerous cells. It divides the cancerous and non-cancerous data sets into different groups. In Search Engines: Search engines also work on the clustering technique. The search result appears based on the closest object to the search query. It does it by grouping similar data objects in one group that is far from the other dissimilar objects. The accurate result of a query depends on the quality of the clustering algorithm used. Customer Segmentation: It is used in market research to segment the customers based on their choice and preferences. In Biology: It is used in the biology stream to classify different species of plants and animals using the image recognition technique. In Land Use: The clustering technique is used in identifying the area of similar lands use in the GIS database. This can be very useful to find that for what purpose the particular land should be used, that means for which purpose it is more suitable.
Reinforcement learning (RL) is an area of machine learning concerned with how intelligent agents ought to take actions in an environment in order to maximize the notion of cumulative reward. Reinforcement learning is one of three basic machine learning paradigms, alongside supervised learning and unsupervised learning.
Reinforcement learning differs from supervised learning in not needing labelled input/output pairs to be presented, and in not needing sub-optimal actions to be explicitly corrected. Instead the focus is on finding a balance between exploration (of uncharted territory) and exploitation (of current knowledge).
The environment is typically stated in the form of a Markov decision process (MDP), because many reinforcement learning algorithms for this context use dynamic programming techniques. The main difference between the classical dynamic programming methods and reinforcement learning algorithms is that the latter do not assume knowledge of an exact mathematical model of the MDP and they target large MDPs where exact methods become infeasible.
Decision tree learning is one of the predictive modelling approaches used in statistics, data mining and machine learning. It uses a decision tree (as a predictive model) to go from observations about an item (represented in the branches) to conclusions about the item's target value (represented in the leaves). It is one of the predictive modelling approaches used in statistics, data mining and machine learning. It uses a decision tree (as a predictive model) to go from observations about an item (represented in the branches) to conclusions about the item's target value (represented in the leaves). It is one of the predictive modelling approaches used in statistics, data mining and machine learning. It uses a decision tree (as a predictive model) to go from observations about an item (represented in the branches) to conclusions about the item's target value (represented in the leaves).
Decision tree learning is one of the predictive modelling approaches used in statistics, data mining and machine learning. It uses a decision tree (as a predictive model) to go from observations about an item (represented in the branches) to conclusions about the item's target value (represented in the leaves). It is one of the predictive modelling approaches used in statistics, data mining and machine learning. It uses a decision tree (as a predictive model) to go from observations about an item (represented in the branches) to conclusions about the item's target value (represented in the leaves). It is one of the predictive modelling approaches used in statistics, data mining and machine learning. It uses a decision tree (as a predictive model) to go from observations about an item (represented in the branches) to conclusions about the item's target value (represented in the leaves).
The decision tree learning algorithm is a supervised learning algorithm that can be used for both classification and regression problems. It is a non-parametric supervised learning method used for classification and regression. It is a non-parametric supervised learning method used for classification and regression. It is a non-parametric supervised learning method used for classification and regression. It is a non-parametric supervised learning method used for classification and regression.
Support vector machines (SVMs) are a set of supervised learning methods used for classification, regression and outliers detection.
Genetic Algorithm (GA) is a search heuristic that is inspired by the process of natural selection. It is a optimization technique used to find the best solution to a problem by mimicking the process of natural selection. Here are some notes on Genetic Algorithm with reference to Machine Learning Techniques:
Definition: A Genetic Algorithm is a search heuristic that is inspired by the process of natural selection. It is used to find the best solution to a problem by mimicking the process of natural selection. Genetic Algorithm starts with a population of solutions called chromosomes, and through the process of selection, crossover, and mutation, it evolves the population to find the best solution.
Components: Genetic Algorithm comprises of the following components:
Population: A set of solutions called chromosomes Fitness Function: A function that measures the quality of a solution Selection: A process of selecting the best chromosomes from the population Crossover: A process of combining two chromosomes to create a new one Mutation: A process of introducing small random changes to a chromosome Termination: A stopping criterion to decide when to stop the algorithm GA cycle of reproduction: Genetic Algorithm follows a cyclic process of reproduction where the following steps are repeated to generate new generations:
Selection: The chromosomes are selected based on their fitness values. Crossover: The selected chromosomes are combined to create new offspring. Mutation: The new offspring are then mutated to introduce randomness and diversity in the population. Applications: Genetic Algorithms are widely used in a variety of applications, including optimization of complex functions, scheduling, game playing and trading, image processing, and pattern recognition.
Examples:
A problem of finding the shortest path between two cities can be solved using genetic algorithm. A problem of finding the global minimum of a function can be solved using genetic algorithm. In conclusion, Genetic Algorithm is a powerful optimization technique that is inspired by the process of natural selection. It can be used to find the best solution to a problem by mimicking the process of natural selection. The flexibility of GA makes it a popular choice among the researchers and practitioners for solving various optimization problems.
Overfitting: Overfitting occurs when a model is trained too well on the training data and performs poorly on new, unseen data. This happens when the model is too complex and is able to memorize the training data instead of learning the underlying patterns. Overfitting can be addressed by using techniques such as regularization, early stopping, and ensembling.
Underfitting: Underfitting occurs when a model is not able to capture the underlying patterns in the data and performs poorly on both the training and the test data. This happens when the model is too simple or when the model is not trained for enough number of iterations. Underfitting can be addressed by using more complex models or increasing the number of iterations.
Lack of Data: In some cases, the availability of labeled data can be a limitation. A model may not be able to generalize well to new data if it is trained on a small dataset. This can be addressed by collecting more data, using data augmentation techniques, or using transfer learning.
Data Quality: In some cases, the quality of the data can be a limitation. A model may not be able to generalize well to new data if the data is noisy, inconsistent, or biased. This can be addressed by data cleaning, data preprocessing and data validation.
Bias: Bias refers to the difference between the model's predictions and the true values for certain groups of data. Bias can occur when the training data is not representative of the population or when the model is not designed to handle certain types of data. This can be addressed by using techniques such as oversampling, undersampling, and data augmentation.
Privacy and Security: Machine Learning models may process sensitive data, which can lead to privacy and security issues. For example, a model that is trained on medical data can be used to discriminate against certain groups of people. This can be addressed by using techniques such as differential privacy, homomorphic encryption and federated learning.
In conclusion, issues in Machine Learning can impact the performance of the model and the overall success of the project. It's important to be aware of these issues and to have strategies in place to address them.
In Machine Learning Techniques, a well-defined learning problem is a problem where the input, output, and desired behavior of the model are clearly specified. A well-defined learning problem is essential for the successful implementation of a machine learning model. Here are some notes on well-defined learning problems with reference to Machine Learning Techniques:
Definition: A well-defined learning problem is a problem where the input, output, and desired behavior of the model are clearly specified. This includes the type of input, the type of output, and the performance criteria for the model.
Examples:
A supervised learning problem where the input is an image and the output is a label indicating whether the image contains a dog or a cat. A supervised learning problem where the input is a customer's historical data and the output is a prediction of whether the customer will churn. A unsupervised learning problem where the input is a set of market transactions and the goal is to find patterns or clusters in the data. Mnemonics: To remember the importance of well-defined learning problems, one can use the mnemonic "CLEAR"
C stands for "clearly defined inputs and outputs" L stands for "learning goal is defined" E stands for "evaluation metric is defined" A stands for "algorithms are chosen based on the problem" R stands for "real-world scenario" Real-world Scenario: In real-world scenarios, a well-defined learning problem is crucial for the successful implementation of machine learning models. For example, in the healthcare industry, a well-defined learning problem would be to predict the likelihood of a patient developing a certain disease based on their medical history and test results. The input would be the patient's medical history and test results, the output would be a probability of the patient developing the disease, and the performance criteria would be the accuracy of the predictions. With a well-defined learning problem, appropriate algorithms can be chosen, and the model can be evaluated using the chosen metric.
In conclusion, a well-defined learning problem is essential for the successful implementation of machine learning models. It allows for the clear specification of inputs, outputs, and desired behavior, which in turn enables the selection of appropriate algorithms and the evaluation of model performance.
Linear regression is one of the easiest and most popular Machine Learning algorithms. It is a statistical method that is used for predictive analysis. Linear regression makes predictions for continuous/real or numeric variables such as sales, salary, age, product price, etc.
Linear regression algorithm shows a linear relationship between a dependent (y) and one or more independent (y) variables, hence called as linear regression. Since linear regression shows the linear relationship, which means it finds how the value of the dependent variable is changing according to the value of the independent variable.
The linear regression model provides a sloped straight line representing the relationship between the variables. Consider the below image:
Linear Regression in Machine Learning Mathematically, we can represent a linear regression as:
y= a0+a1x+ ε Here,
Y= Dependent Variable (Target Variable) X= Independent Variable (predictor Variable) a0= intercept of the line (Gives an additional degree of freedom) a1 = Linear regression coefficient (scale factor to each input value). ε = random error
The values for x and y variables are training datasets for Linear Regression model representation.
Types of Linear Regression Linear regression can be further divided into two types of the algorithm:
Simple Linear Regression:
If a single independent variable is used to predict the value of a numerical dependent variable, then such a Linear Regression algorithm is called Simple Linear Regression. Multiple Linear regression: If more than one independent variable is used to predict the value of a numerical dependent variable, then such a Linear Regression algorithm is called Multiple Linear Regression. Linear Regression Line A linear line showing the relationship between the dependent and independent variables is called a regression line. A regression line can show two types of relationship:
Positive Linear Relationship: If the dependent variable increases on the Y-axis and independent variable increases on X-axis, then such a relationship is termed as a Positive linear relationship. Linear Regression in Machine Learning Negative Linear Relationship: If the dependent variable decreases on the Y-axis and independent variable increases on the X-axis, then such a relationship is called a negative linear relationship. Linear Regression in Machine Learning Finding the best fit line: When working with linear regression, our main goal is to find the best fit line that means the error between predicted values and actual values should be minimized. The best fit line will have the least error.
The different values for weights or the coefficient of lines (a0, a1) gives a different line of regression, so we need to calculate the best values for a0 and a1 to find the best fit line, so to calculate this we use cost function.
Cost function- The different values for weights or coefficient of lines (a0, a1) gives the different line of regression, and the cost function is used to estimate the values of the coefficient for the best fit line. Cost function optimizes the regression coefficients or weights. It measures how a linear regression model is performing. We can use the cost function to find the accuracy of the mapping function, which maps the input variable to the output variable. This mapping function is also known as Hypothesis function. For Linear Regression, we use the Mean Squared Error (MSE) cost function, which is the average of squared error occurred between the predicted values and actual values. It can be written as:
For the above linear equation, MSE can be calculated as:
Linear Regression in Machine Learning Where,
N=Total number of observation Yi = Actual value (a1xi+a0)= Predicted value.
Residuals: The distance between the actual value and predicted values is called residual. If the observed points are far from the regression line, then the residual will be high, and so cost function will high. If the scatter points are close to the regression line, then the residual will be small and hence the cost function.
Gradient Descent: Gradient descent is used to minimize the MSE by calculating the gradient of the cost function. A regression model uses gradient descent to update the coefficients of the line by reducing the cost function. It is done by a random selection of values of coefficient and then iteratively update the values to reach the minimum cost function. Model Performance: The Goodness of fit determines how the line of regression fits the set of observations. The process of finding the best model out of various models is called optimization. It can be achieved by below method:
R-squared is a statistical method that determines the goodness of fit. It measures the strength of the relationship between the dependent and independent variables on a scale of 0-100%. The high value of R-square determines the less difference between the predicted values and actual values and hence represents a good model. It is also called a coefficient of determination, or coefficient of multiple determination for multiple regression. It can be calculated from the below formula: Linear Regression in Machine Learning Assumptions of Linear Regression Below are some important assumptions of Linear Regression. These are some formal checks while building a Linear Regression model, which ensures to get the best possible result from the given dataset.
Linear relationship between the features and target: Linear regression assumes the linear relationship between the dependent and independent variables. Small or no multicollinearity between the features: Multicollinearity means high-correlation between the independent variables. Due to multicollinearity, it may difficult to find the true relationship between the predictors and target variables. Or we can say, it is difficult to determine which predictor variable is affecting the target variable and which is not. So, the model assumes either little or no multicollinearity between the features or independent variables. Homoscedasticity Assumption: Homoscedasticity is a situation when the error term is the same for all the values of independent variables. With homoscedasticity, there should be no clear pattern distribution of data in the scatter plot. Normal distribution of error terms: Linear regression assumes that the error term should follow the normal distribution pattern. If error terms are not normally distributed, then confidence intervals will become either too wide or too narrow, which may cause difficulties in finding coefficients. It can be checked using the q-q plot. If the plot shows a straight line without any deviation, which means the error is normally distributed. No autocorrelations: The linear regression model assumes no autocorrelation in error terms. If there will be any correlation in the error term, then it will drastically reduce the accuracy of the model. Autocorrelation usually occurs if there is a dependency between residual errors.
Logistic Regression is a supervised learning algorithm used for classification problems. It is a statistical method that is used to model the relationship between a set of independent variables and a binary dependent variable. Here are some notes on Logistic Regression:
Definition: Logistic Regression is a statistical method that is used to model the relationship between a set of independent variables and a binary dependent variable. The goal is to find the best set of parameters that maximizes the likelihood of the observed data.
Model: Logistic Regression models the probability of the binary outcome as a function of the input features using the logistic function (sigmoid function). The logistic function produces an output between 0 and 1, which can be interpreted as a probability of the binary outcome. The parameters of the model are learned by maximizing the likelihood of the observed data.
Training: The training process of logistic regression is iterative, it starts with an initial set of parameters, then it uses optimization algorithm like gradient descent to iteratively update the parameters to maximize the likelihood of the observed data.
Evaluation Metrics: The performance of logistic regression models can be evaluated using metrics such as accuracy, precision, recall, and F1-score.
Applications: Logistic Regression is widely used in a variety of applications, including image classification, natural language processing, and bioinformatics.
Examples:
A logistic regression model that is used to predict whether an email is spam or not spam, based on the presence of certain keywords in the email. A logistic regression model that is used to predict whether a patient has a certain disease based on their symptoms and test results. In conclusion, Logistic Regression is a widely used algorithm for classification problems. It models the probability of a binary outcome as a function of the input features using the logistic function, and the parameters of the model are learned by maximizing the likelihood of the observed data. It's simple, easy to implement and can provide good results for a large number of problems.
Bayesian Learning is a statistical learning method based on Bayesian statistics and probability theory. It is used to update the beliefs about the state of the world based on new evidence. Here are some notes on Bayesian Learning:
Definition: Bayesian Learning is a statistical learning method based on Bayesian statistics and probability theory. The goal is to update the beliefs about the state of the world based on new evidence.
Bayes Theorem: Bayesian Learning is based on Bayes' theorem, which states that the probability of a hypothesis given some data (P(H|D)) is proportional to the probability of the data given the hypothesis (P(D|H)) multiplied by the prior probability of the hypothesis (P(H)). Bayes' theorem is often written as P(H|D) = P(D|H) * P(H) / P(D)
Prior and Posterior: In Bayesian Learning, a prior probability distribution is specified for the model parameters, which encodes our prior knowledge or beliefs about the parameters. When new data is observed, the prior is updated to form a posterior probability distribution, which encodes our updated beliefs about the parameters given the data.
Conjugate Prior: To make the calculation of the posterior distribution simple and efficient, it is often useful to use a conjugate prior distribution, which is a distribution that is mathematically related to the likelihood function.
Applications: Bayesian Learning is widely used in a variety of applications, including natural language processing, computer vision, and bioinformatics.
Examples:
A Bayesian Learning model that is used to predict whether a patient has a certain disease based on their symptoms and test results. The prior probability distribution encodes our beliefs about the prevalence of the disease in the population, and the likelihood function encodes the probability of observing the symptoms and test results given the disease. A Bayesian Learning model that is used to estimate the parameters of a robot's sensor model, by updating the beliefs about the sensor model based on the robot's sensor readings. In conclusion, Bayesian Learning is a statistical learning method based on Bayesian statistics and probability theory. It is used to update the beliefs about the state of the world based on new evidence. It's powerful and flexible and can be used for a wide range of problems. However, it can be computationally expensive and requires a good understanding of probability theory to implement it correctly.
Bayes' theorem is a fundamental result in probability theory that relates the conditional probability of an event to the prior probability of the event and the likelihood of the event given some other information. Here are some notes on Bayes' theorem:
Definition: Bayes' theorem states that the conditional probability of an event A given that another event B has occurred is proportional to the prior probability of event A and the likelihood of event B given event A. Mathematically, it can be written as: P(A|B) = (P(B|A) * P(A)) / P(B)
Intuition: Bayes' theorem is useful for updating our beliefs about the probability of an event given new information. The prior probability is our initial belief before we see the new information, the likelihood is how likely the new information is given our prior belief, and the posterior probability is our updated belief after we see the new information.
Applications: Bayes' theorem has many applications in machine learning, specifically in the field of Bayesian learning. It can be used for classification problems, where the goal is to find the class label of a given input based on the class probabilities and the likelihood of the input given each class. It can also be used for parameter estimation problems, where the goal is to estimate the values of model parameters given some data.
Example:
A weather forecaster states that there is a 30% chance of rain tomorrow, and you observe that it is cloudy today. According to Bayes' theorem, the probability of rain tomorrow given that it is cloudy today can be calculated as: P(Rain|Cloudy) = (P(Cloudy|Rain) * P(Rain)) / P(Cloudy) Here, P(Rain|Cloudy) is the posterior probability, P(Cloudy|Rain) is the likelihood, P(Rain) is the prior probability and P(Cloudy) is the normalizing constant. In conclusion, Bayes' theorem is a fundamental result in probability theory that relates the conditional probability of an event to the prior probability of the event and the likelihood of the event given some other information. It provides a way to update our beliefs about the probability of an event given new information and has many applications in machine learning, particularly in the field of Bayesian learning.
Bayes theorem is a mathematical formula that describes the probability of an event, based on prior knowledge of conditions that might be related to the event. Here are some notes on Bayes theorem:
Definition: Bayes theorem is a mathematical formula that describes the probability of an event, based on prior knowledge of conditions that might be related to the event. It is named after the Reverend Thomas Bayes, who published a paper on the theorem in 1763.
Bayes Theorem: Bayes theorem states that the probability of an event (A) given some evidence (B) is proportional to the probability of the evidence (B) given the event (A) multiplied by the prior probability of the event (A). Bayes theorem is often written as P(A|B) = P(B|A) * P(A) / P(B)
Concept learning, also known as concept formation, is a process of learning a general rule or concept from a set of examples. It is a type of unsupervised learning where the goal is to identify the underlying structure or pattern in the data without any prior knowledge of the output. Here are some notes on Concept learning:
Definition: Concept learning is a type of unsupervised learning where the goal is to identify the underlying structure or pattern in the data without any prior knowledge of the output. It is a process of learning a general rule or concept from a set of examples.
Inductive Inference: Concept learning is based on the process of inductive inference. Inductive inference is the process of making generalizations from specific examples. In concept learning, the model uses the examples to infer a general rule or concept that explains the relationship between the input and output.
Concept Learning Algorithms: There are several algorithms used for concept learning, including decision trees, rule-based systems, and nearest-neighbor methods.
Decision Trees: Decision trees are a popular algorithm for concept learning. They use a tree structure to represent the possible concepts and make decisions based on the input.
Rule-based Systems: Rule-based systems use a set of if-then rules to represent the concepts. The rules are learned from the examples and can be used to classify new examples.
Nearest-neighbor Methods: Nearest-neighbor methods are based on the idea that similar examples have similar concepts. The model classifies new examples based on the most similar examples in the training set.
Evaluation Metrics: The performance of concept learning models can be evaluated using metrics such as accuracy, precision, recall, and F1-score.
Applications: Concept learning algorithms are widely used in a variety of applications, including natural language processing, computer vision, speech recognition, and bioinformatics.
Limitations: Concept learning algorithms can be limited by the quality and representativeness of the training data, and may not be able to generalize well to new, unseen data. Additionally, the results of concept learning can be hard to interpret, and the discovered concepts may not be meaningful.
In conclusion, Concept learning is a process of unsupervised learning where the goal is to identify the underlying structure or pattern in the data without any prior knowledge of the output. It is based on the process of inductive inference and several algorithms, such as decision trees, rule-based systems, and nearest-neighbor methods are used to implement it. It's used in several applications and has its own set of limitations and challenges.
The Bayes Optimal Classifier (BOC) is a theoretical classifier that makes the best possible predictions based on the probability of the input data. It is a type of Bayesian classifier that is based on Bayes' theorem, which states that the probability of an event occurring is equal to the prior probability of the event multiplied by the likelihood of the event given certain observations. Here are some notes on the Bayes Optimal Classifier:
Definition: The Bayes Optimal Classifier (BOC) is a theoretical classifier that makes the best possible predictions based on the probability of the input data. It is based on Bayes' theorem and is considered the "gold standard" for classification tasks.
Bayes' Theorem: BOC is based on Bayes' theorem, which states that the probability of an event occurring is equal to the prior probability of the event multiplied by the likelihood of the event given certain observations. In the context of classification, the BOC uses the likelihood of the input data given certain class labels and the prior probability of the class labels to make predictions.
Assumptions: The BOC makes the assumption that the data is generated by a probabilistic process and that the class labels and input features are independent. Additionally, it assumes that the probability distributions of the input data are known.
Evaluation Metrics: The BOC is considered to be the best possible classifier in terms of accuracy, as it makes predictions based on the true underlying probability distributions of the data.
Applications: The BOC is mainly used as a theoretical benchmark for comparing the performance of other classifiers.
Limitations: The BOC is not practical to use in in real-world scenarios, as it requires knowledge of the true underlying probability distributions of the data, which is often not available. Additionally, the BOC can be computationally expensive, as it requires the calculation of the likelihood and prior probabilities for all possible class labels for each input.
Real-world Scenario: In real-world scenarios, the BOC is not practical to use. For example, in the healthcare industry, a doctor may not have the knowledge of the true underlying probability distributions of a patient's medical history and test results to make the best possible predictions about their disease. However, the BOC can be used as a benchmark to evaluate the performance of other classifiers, such as logistic regression or decision trees. In conclusion, The Bayes Optimal Classifier (BOC) is a theoretical classifier that makes the best possible predictions based on the probability of the input data. It is based on Bayes' theorem, and it's considered the "gold standard" for classification tasks, but it's not practical to use in real-world scenarios as it requires knowledge of the true underlying probability distributions of the data, which is often not available, and it can be computationally expensive. It is mainly used as a theoretical benchmark for comparing the performance of other classifiers.
Naive Bayes classifier is a probabilistic algorithm based on Bayes theorem for classification tasks. It is a simple and efficient algorithm that makes the naive assumption that all the features are independent from each other. Here are some notes on Naive Bayes classifier:
Definition: Naive Bayes classifier is a probabilistic algorithm based on Bayes theorem for classification tasks. It makes the naive assumption that all the features are independent from each other and uses this assumption to calculate the probability of a class given the input features.
Bayes theorem: Bayes theorem states that the probability of a hypothesis (H) given some evidence (E) is proportional to the probability of the evidence given the hypothesis (P(E|H)) multiplied by the prior probability of the hypothesis (P(H)). In the case of Naive Bayes classifier, the hypothesis is the class, and the evidence is the input features.
Types of Naive Bayes Classifier: There are several types of Naive Bayes classifiers, including Gaussian Naive Bayes, Multinomial Naive Bayes, and Bernoulli Naive Bayes.
Gaussian Naive Bayes: This algorithm assumes that the data is normally distributed and calculates the likelihood of the data given the class using the Gaussian distribution.
Multinomial Naive Bayes: This algorithm is used for discrete data, such as text data. It calculates the likelihood of the data given the class using the multinomial distribution.
Bernoulli Naive Bayes: This algorithm is also used for discrete data, such as binary data. It calculates the likelihood of the data given the class using the Bernoulli distribution.
Training: The training process of Naive Bayes classifier is relatively simple. It involves calculating the prior probability of each class and the likelihood of each feature given each class. These probabilities are then used to calculate the posterior probability of each class given the input features. The class with the highest posterior probability is chosen as the final prediction.
Evaluation Metrics: The performance of Naive Bayes classifier can be evaluated using metrics such as accuracy, precision, recall, and F1-score.
Applications: Naive Bayes classifier is widely used in a variety of applications, including text classification, spam filtering, and sentiment analysis.
Limitations: The naive assumption of independence between features can lead to poor performance in cases where the features are highly dependent on each other. Additionally, the performance of Naive Bayes classifier can be sensitive to the presence of irrelevant features and outliers in the data.
In conclusion, Naive Bayes classifier is a simple and efficient algorithm for classification tasks that is based on Bayes theorem. It makes the naive assumption that all the features are independent from each other and uses this assumption to calculate the probability of a class given the input features. It's widely used in several applications, but its performance can be affected by certain factors such as the independence assumption and presence of irrelevant features.
Bayesian belief networks (BBN), also known as Bayesian networks or Belief networks, are probabilistic graphical models that represent the relationships between variables and their probability distributions. They are based on Bayes theorem and are used for reasoning under uncertainty. Here are some notes on Bayesian belief networks:
Definition: Bayesian belief networks (BBN) are probabilistic graphical models that represent the relationships between variables and their probability distributions. They are used for reasoning under uncertainty, and are based on Bayes theorem. BBN represents a set of variables and their conditional dependencies via a directed acyclic graph (DAG). Each node in the graph represents a variable, and each directed edge represents the conditional dependency between two variables.
Conditional Probability: Bayesian belief networks use conditional probability to model the relationships between variables. The probability of a variable given its parents in the graph is represented by a conditional probability distribution. This allows the model to represent the dependencies between variables and how they affect each other.
Inference: Inference in BBN is the process of computing the probability of a variable given the observed values of other variables. This can be done using exact methods such as variable elimination or approximate methods such as Markov Chain Monte Carlo (MCMC).
Learning: Learning in BBN involves estimating the parameters of the conditional probability distributions given a dataset. This can be done using methods such as Maximum Likelihood Estimation (MLE) or Expectation Maximization (EM).
Applications: Bayesian belief networks are widely used in a variety of applications, including medical diagnosis, bioinformatics, natural language processing and computer vision.
Limitations: Bayesian belief networks can be computationally expensive for large datasets or complex models. Additionally, they can be sensitive to missing or noisy data and may not work well for non-linear relationships.
In conclusion, Bayesian belief networks (BBN) are probabilistic graphical models that are used for reasoning under uncertainty. They represent the relationships between variables and their probability distributions via a directed acyclic graph (DAG). They are based on Bayes theorem and can be used for inference and learning. They are widely used in several applications, but they can be computationally expensive for large datasets or complex models.
The Expectation-Maximization (EM) algorithm is an iterative method used for finding maximum likelihood estimates of parameters in models where the data is incomplete or has missing values. It is a widely used technique for estimating parameters in latent variable models, including mixture models and hidden Markov models. Here are some notes on the EM algorithm:
Definition: The Expectation-Maximization (EM) algorithm is an iterative method used for finding maximum likelihood estimates of parameters in models where the data is incomplete or has missing values. It is a widely used technique for estimating parameters in latent variable models, including mixture models and hidden Markov models.
Iterative Process: The EM algorithm consists of two steps: the expectation step (E-step) and the maximization step (M-step). In the E-step, the algorithm estimates the expectation of the complete data log-likelihood function, given the current parameter estimates. In the M-step, the algorithm maximizes the expected complete data log-likelihood function with respect to the parameters, using the estimates from the E-step. This process is repeated until the parameters converge to a maximum likelihood estimate.
Latent Variables: The EM algorithm is particularly useful for models that have latent variables, which are variables that are not directly observed but are inferred from the observed data. Examples of latent variables include the hidden states in a hidden Markov model, or the component membership in a mixture model.
Applications: The EM algorithm is widely used in a variety of applications, including natural language processing, computer vision, bioinformatics, and finance.
Limitations: The EM algorithm can be sensitive to the initialization of the parameters and can converge to a local maximum, rather than the global maximum. Additionally, it can be computationally expensive for large datasets or complex models.
In conclusion, the Expectation-Maximization (EM) algorithm is an iterative method used for finding maximum likelihood estimates of parameters in models where the data is incomplete or has missing values. It is widely used for estimating parameters in latent variable models and is particularly useful for models that have latent variables. It has its own set of limitations and challenges, and its performance can be affected by certain factors such as initialization of the parameters and computational complexity.
Support Vector Machine (SVM) is a supervised learning algorithm used for classification and regression problems. It is a powerful algorithm that can model non-linear decision boundaries by using kernel functions. Here are some notes on Support Vector Machine:
Definition: Support Vector Machine (SVM) is a supervised learning algorithm used for classification and regression problems. It is a powerful algorithm that can model non-linear decision boundaries by using kernel functions. The goal of the SVM algorithm is to find the best decision boundary, called the hyperplane, that separates the data into different classes.
Linear SVM: SVM can be used for linear classification problems, where the decision boundary is a straight line or a hyperplane. In this case, the algorithm finds the hyperplane that maximizes the margin, which is the distance between the decision boundary and the closest data points from each class. These closest data points are called support vectors.
Non-linear SVM: SVM can also be used for non-linear classification problems, where the decision boundary is not a straight line or a hyperplane. In this case, the algorithm uses a kernel function to map the input data into a higher-dimensional space where a linear decision boundary can be found. Some commonly used kernel functions are the polynomial kernel, radial basis function (RBF) kernel, and sigmoid kernel.
Training: The training process of SVM involves solving a convex optimization problem to find the optimal hyperplane. The objective is to maximize the margin while keeping the misclassification errors as low as possible.
Evaluation Metrics: The performance of SVM can be evaluated using metrics such as accuracy, precision, recall, and F1-score.
Applications: SVM is widely used in a variety of applications, including image classification, natural language processing, and bioinformatics.
Limitations: SVM can be sensitive to the choice of kernel function, and the model may not converge to the optimal solution in case of noisy or non-separable data. Additionally, SVM can be computationally intensive for large datasets and may not scale well to high-dimensional data.
In conclusion, Support Vector Machine (SVM) is a powerful algorithm for classification and regression problems that can model non-linear decision boundaries using kernel functions. It finds the best decision boundary, called the hyperplane, that separates the data into different classes by maximizing the margin. SVM is widely used in several applications but has certain limitations such as sensitivity to kernel function, computational intensity, and non-convergence in case of noisy data.
Support Vector Machine (SVM) is a supervised learning algorithm that can be used for both classification and regression tasks. One of the key features of SVM is the use of kernel functions, which map the input data into a higher dimensional space in order to find a hyperplane that separates the classes. Here are some notes on the types of support vector kernel:
Linear kernel: The linear kernel is the simplest kernel function and it maps the input data into a linear space. It is defined as the dot product between the input vectors. It is useful when the data is linearly separable.
Polynomial kernel: The polynomial kernel maps the input data into a polynomial space. It is defined as the dot product between the input vectors raised to a power. It can be used when the data is not linearly separable, and it can be useful when the data has a non-linear decision boundary.
Gaussian kernel (RBF): The Gaussian kernel, also known as the radial basis function (RBF) kernel, maps the input data into an infinite-dimensional space. It is defined as the exponential of the negative squared Euclidean distance between the input vectors. It is commonly used in SVM and it is known to work well on a wide range of problems.
Sigmoid kernel: The sigmoid kernel maps the input data into a sigmoid space. It is defined as the tanh of the dot product between the input vectors and a set of parameters. It is less commonly used than the other types of kernels and it is generally used in cases where the data has a non-linear decision boundary.
String kernel: String kernel is a kernel that operates on the sequence of symbols, in this case, the kernel computes the similarity between two strings by counting the number of common substrings. String kernel can be used in text classification and bioinformatics.
In conclusion, the choice of kernel function is an important aspect of SVM algorithm and it can greatly affect the performance of the model. The linear kernel is the simplest and it is useful when the data is linearly separable. The polynomial and Gaussian kernels can be used when the data is not linearly separable and they are commonly used in SVM. The sigmoid kernel is less commonly used and it is generally used in cases where the data has a non-linear decision boundary. String kernel is used in specific applications like text classification and bioinformatics.
The linear kernel is a kernel function used in Support Vector Machine (SVM) that maps the input data into a linear space. It is the simplest kernel function and it is defined as the dot product between the input vectors. Here are some notes on the linear kernel:
Definition: The linear kernel is a kernel function used in Support Vector Machine (SVM) that maps the input data into a linear space. It is defined as the dot product between the input vectors. It is the simplest kernel function used in SVM.
Linear Separability: The linear kernel is useful when the data is linearly separable. In other words, when there exists a linear boundary that can separate the classes. In this case, the linear kernel can find a hyperplane that separates the classes in the original input space.
Computational Efficiency: The linear kernel has the advantage of being computationally efficient. The dot product between two vectors can be computed in O(n) time, where n is the number of features in the input data. This makes it suitable for large datasets or real-time applications.
Limitations: The linear kernel has some limitations when applied to non-linearly separable data. It can't capture complex relationships between the input features and the output classes, and it may not be able to find a good boundary that separates the classes.
Real-world Applications: The linear kernel is widely used in a variety of applications such as text classification, image classification, speech recognition and bioinformatics.
In conclusion, the linear kernel is a kernel function used in SVM, it is defined as the dot product between the input vectors, and it is useful when the data is linearly separable, it has the advantage of being computationally efficient and it is widely used in a variety of applications, but it has limitations when applied to non-linearly separable data.
The polynomial kernel is a kernel function used in Support Vector Machine (SVM) algorithm that maps the input data into a higher-dimensional polynomial space. This can be useful when the data is not linearly separable, as it can help to find a hyperplane that separates the classes. Here are some more details on polynomial kernel:
Definition: The polynomial kernel is defined as the dot product between the input vectors raised to a power. It is represented as K(x,x') = (x.x' + c)^d, where x and x' are the input vectors, c is a constant, and d is the degree of the polynomial.
Parameters: The polynomial kernel has three parameters: the degree of the polynomial (d), the constant term (c) and the coefficient term (coef0). The degree of the polynomial (d) controls the complexity of the decision boundary, the constant term (c) controls the trade-off between maximizing the margin and minimizing the classification error, and the coefficient term (coef0) is used to change the bias-variance trade-off.
Non-linear decision boundary: The polynomial kernel can be used when the data is not linearly separable and it can help to find a non-linear decision boundary that separates the classes. The decision boundary created by the polynomial kernel can be more complex than that created by the linear kernel and it can be more suitable for data with a non-linear decision boundary.
Overfitting: If the degree of the polynomial is too high, the polynomial kernel can lead to overfitting. Overfitting occurs when the model is too complex and it fits the noise in the data rather than the underlying pattern. To avoid overfitting, it's important to choose a good value for the degree of the polynomial and also to use cross-validation to choose the best parameters.
Applications: The polynomial kernel is widely used in a variety of applications, such as image classification, text classification, and bioinformatics.
In conclusion, The polynomial kernel is a kernel function that maps the input data into a higher-dimensional polynomial space. It's useful when the data is not linearly separable and can help to find a non-linear decision boundary that separates the classes. The polynomial kernel has several parameters, such as degree of the polynomial, constant term and the coefficient term. It's important to choose a good value for the degree of the polynomial to avoid overfitting and also to use cross-validation to choose the best parameters. It's widely used in several applications.
The Gaussian kernel, also known as the radial basis function (RBF) kernel, is a kernel function used in Support Vector Machine (SVM) that maps the input data into an infinite-dimensional space. It is defined as the exponential of the negative squared Euclidean distance between the input vectors. Here are some notes on the Gaussian kernel:
Definition: The Gaussian kernel, also known as the radial basis function (RBF) kernel, is a kernel function used in Support Vector Machine (SVM) that maps the input data into an infinite-dimensional space. It is defined as the exponential of the negative squared Euclidean distance between the input vectors.
Non-linear Separability: The Gaussian kernel is useful when the data is not linearly separable. In other words, when there does not exist a linear boundary that can separate the classes. In this case, the Gaussian kernel can find a boundary that separates the classes in an infinite-dimensional space.
Computational Efficiency: The Gaussian kernel is computationally efficient. Computing the Euclidean distance between two vectors can be done in O(n) time, where n is the number of features in the input data. This makes it suitable for large datasets or real-time applications.
Limitations: One of the main limitations of the Gaussian kernel is its sensitivity to the choice of the kernel's hyperparameter, which determines the width of the Gaussian. If the hyperparameter is set too high, the decision boundary will be too broad and the model will overfit, if it is set too low, the decision boundary will be too narrow and the model will underfit. This can make it difficult to find an optimal value for the hyperparameter. Additionally, Gaussian kernel is computationally expensive for high-dimensional data, as it requires a lot of memory to store the kernel matrix.
Real-world Applications: The Gaussian kernel is widely used in a variety of applications such as text classification, image classification, speech recognition and bioinformatics
A hyperplane is a mathematical concept that is often used in machine learning and specifically in the support vector machine (SVM) algorithm. In simple terms, a hyperplane is a multidimensional line that is used to separate different classes or groups of data points. The goal of the SVM algorithm is to find the best hyperplane that separates the data points into their respective classes with the maximum margin.
In a two-dimensional space, a hyperplane is a line that separates the data points into two classes. However, in higher-dimensional spaces, a hyperplane becomes a hyperplane in n-dimensional space. For example, in a three-dimensional space, a hyperplane is a plane that separates the data points into two classes. In a four-dimensional space, a hyperplane is a hyperplane in four-dimensional space, and so on.
The SVM algorithm uses the concept of a hyperplane to separate the data points into their respective classes. The algorithm begins by finding the hyperplane that separates the data points with the maximum margin. The margin is the distance between the hyperplane and the closest data points from each class. The goal of the SVM algorithm is to find the hyperplane that maximizes the margin between the data points.
The SVM algorithm uses a technique called the kernel trick to find the best hyperplane. The kernel trick is a mathematical technique that allows the SVM algorithm to find the best hyperplane even in higher-dimensional spaces. The kernel trick maps the data points into a higher-dimensional space, where it is easier to find the best hyperplane.
In summary, a hyperplane is a mathematical concept that is used in the SVM algorithm to separate different classes of data points. The goal of the SVM algorithm is to find the best hyperplane that separates the data points into their respective classes with the maximum margin. The SVM algorithm uses a technique called the kernel trick to find the best hyperplane even in higher-dimensional spaces.
Definition: A hyperplane is a subspace that is one dimension lower than the original space. For example, a line is a 1-dimensional hyperplane, a plane is a 2-dimensional hyperplane, and a hyperplane is a 3-dimensional hyperplane. The hyperplane is a linear subspace that separates the input space into two parts.
Separating Hyperplane: In the context of Support Vector Machine (SVM), the hyperplane is a linear subspace that separates the input space into two parts. This is done by maximizing the margin between the hyperplane and the nearest points in each class.
Real-world Applications: The hyperplane is widely used in a variety of applications such as text classification, image classification, speech recognition and bioinformatics.
In conclusion, the hyperplane is a subspace that is one dimension lower than the original space, it is a linear subspace that separates the input space into two parts, and it is widely used in a variety of applications.
Support Vector Machines (SVMs) are a type of supervised learning algorithm that can be used for classification or regression tasks. Here are some of the key properties of SVMs:
Linear and Non-linear classification: SVMs can be used for both linear and non-linear classification tasks. For linear classification, the decision boundary is a hyperplane. For non-linear classification, the decision boundary is created by transforming the data into a higher-dimensional space where it becomes linearly separable.
Maximal Margin Classifier: The decision boundary that maximizes the margin, which is the distance between the closest data points of different classes, is chosen as the optimal boundary.
Support Vectors: The data points that are closest to the decision boundary are called support vectors. These are the data points that have the most influence on the position of the boundary.
Regularization: SVMs use a regularization parameter, called C, to control the trade-off between maximizing the margin and minimizing the classification error.
Kernel Trick: The kernel trick is a technique used to transform non-linearly separable data into a higher-dimensional space where it becomes linearly separable. This can be done by using different types of kernel functions, such as the polynomial kernel, radial basis function kernel, and sigmoid kernel.
Versatility: SVMs can be used for various type of classification problem, like text classification, image classification, speech recognition, and bioinformatics.
Robustness: SVMs are relatively robust to noise and outliers, as the decision boundary is based on the support vectors, which are the data points closest to the boundary.
Sparse Solution: SVMs tend to find a sparse solution, which means that only a subset of the training data points are used as support vectors. This makes SVMs memory efficient and fast to train.
It's important to note that while SVMs are powerful and versatile models, they can be sensitive to the choice of kernel function, and the choice of the regularization parameter. However, some libraries like scikit-learn have grid search algorithm to help finding the best parameters.
Support Vector Machines (SVMs) are a popular supervised learning algorithm for classification and regression problems. However, there are a few issues that can arise when using SVMs. Here are some of them:
The choice of kernel: The kernel is a function that maps the input data into a higher-dimensional space, where it is easier to find a linear boundary. Choosing an appropriate kernel can be challenging, as different kernels may perform better or worse depending on the specific problem.
Overfitting: SVMs are prone to overfitting when the number of features is larger than the number of samples. To avoid overfitting, regularization techniques such as the use of soft margins or the addition of a penalty term to the cost function can be used.
Computational complexity: SVMs are computationally expensive, especially when the number of samples is large. This can make training and testing SVMs impractical for large datasets.
High-dimensional problems: When the dimensionality of the problem is high, the number of samples required to achieve good generalization can be prohibitively large. This can make SVMs less effective for high-dimensional problems.
Non-linearly separable problems: SVMs are designed to find linear decision boundaries, and may perform poorly on non-linearly separable problems. To address this, kernel trick can be used to map the data into a higher dimensional space in which a linear boundary can be found.
Handling multi-class problems: SVMs are primarily designed for binary classification problems. To handle multi-class problems, various techniques such as one-vs-all or one-vs-one can be used.
Lack of probabilistic output: SVMs do not provide probabilistic output, which makes it difficult to estimate the uncertainty of the predictions.
Handling missing data: SVMs cannot handle missing data. This can be a problem when working with datasets that have missing values.
To overcome these issues, it is important to carefully tune the parameters of the SVM, and to consider other algorithms such as neural networks, decision trees, and random forests that may be more appropriate for the problem at hand.
Decision tree learning is a method for creating a model that can be used to make predictions or decisions. It is a type of supervised learning algorithm that can be used for both classification and regression problems.
A decision tree is a flowchart-like tree structure, where each internal node represents a feature or attribute, each branch represents a decision or rule, and each leaf node represents the outcome or a class label. The topmost node in the decision tree is called the root node, and the bottommost nodes are called leaf nodes.
The process of creating a decision tree involves repeatedly splitting the training data into subsets based on the values of the input features. The goal is to create subsets (or "leaves") that are as pure as possible, meaning that they contain only examples of one class. The splits are chosen so as to maximize a criterion such as information gain or Gini impurity. The resulting tree can then be used to make predictions on new examples by traversing the tree from the root to a leaf node, using the decision rules at each internal node.
There are several algorithms for building decision trees, including:
ID3 (Iterative Dichotomiser 3): This is an early decision tree algorithm that uses information gain to select the best feature to split on at each node.
C4.5: This is an extension of ID3 that can handle both categorical and numerical features. It also uses information gain to select the best feature to split on.
CART (Classification and Regression Trees): This algorithm can be used for both classification and regression problems. It uses Gini impurity as the splitting criterion.
Random Forest: This is an ensemble learning method that generates multiple decision trees and combines their predictions to improve the overall performance.
Decision trees have several advantages over other algorithms such as:
They are easy to understand and interpret. They can handle both categorical and numerical features. They can handle missing data. They can handle large datasets. However, decision trees also have some disadvantages such as:
They can easily overfit the training data, especially when the tree is deep. They can be sensitive to small changes in the training data. They can be biased towards features with many levels. To overcome these issues, various techniques such as pruning, bagging, and boosting can be used to improve the performance of decision trees.
Decision tree learning is a supervised machine learning algorithm that can be used for both classification and regression problems. It creates a model in the form of a tree structure, where each internal node represents a feature or attribute, each branch represents a decision or rule, and each leaf node represents the outcome or a class label.
The basic algorithm for decision tree learning can be broken down into the following steps:
Select the root node: The root node represents the feature that best splits the data into subsets with the highest purity. The purity of a subset is measured by a criterion such as information gain or Gini impurity.
Create internal nodes: For each subset created in the previous step, repeat the process of selecting the feature that best splits the data into subsets with the highest purity.
Create leaf nodes: Once a subset can no longer be split, it becomes a leaf node. The class label of the majority of examples in the subset is assigned to the leaf node.
Prune the tree: To avoid overfitting, the tree can be pruned by removing branches that do not improve the overall performance.
The most popular algorithms for building decision trees include ID3, C4.5, and CART (Classification and Regression Trees).
ID3 (Iterative Dichotomiser 3) is an early decision tree algorithm that uses information gain as the criterion for selecting the best feature to split on at each node. Information gain measures the decrease in entropy (or uncertainty) of the class labels after a feature is used to split the data.
C4.5 is an extension of ID3 that can handle both categorical and numerical features. It also uses information gain as the criterion for selecting the best feature to split on.
CART (Classification and Regression Trees) can be used for both classification and regression problems. It uses Gini impurity as the criterion for selecting the best feature to split on. Gini impurity measures the probability of a randomly chosen example being misclassified if its class label is randomly assigned based on the class distribution of the examples in a subset.
The decision tree algorithm has several advantages, such as ease of interpretation and handling both categorical and numerical features. However, it also has some disadvantages, such as overfitting, sensitivity to small changes in the data and bias towards features with many levels. To overcome these issues, various techniques such as pruning, bagging, and boosting can be used to improve the performance of decision trees.
Inductive bias refers to the assumptions and preconceptions that a machine learning algorithm has about the data it is processing. These biases can affect the algorithm's ability to generalize from the training data to new, unseen data.
Inductive bias can be divided into two main types: positive and negative. Positive inductive bias refers to the assumption that the data follows a certain pattern or structure, which can help the algorithm learn more efficiently. For example, a decision tree algorithm has a positive inductive bias towards hierarchically organized data, as it allows the algorithm to make more efficient splits at each node.
On the other hand, negative inductive bias refers to the assumption that the data does not follow a certain pattern or structure, which can lead to the algorithm missing important information. For example, a linear regression algorithm has a negative inductive bias towards non-linear data, as it assumes that the relationship between the input and output is linear, and may not be able to capture more complex relationships.
It is important to note that while inductive bias can be limiting, it is also necessary for any machine learning algorithm to make predictions. Without any assumptions about the data, the algorithm would have to consider all possible hypotheses, making it computationally infeasible.
The choice of algorithm and its corresponding inductive bias should be chosen based on the nature of the problem and the characteristics of the data. For example, decision tree algorithms are well suited for classification problems with hierarchically organized data, while linear regression algorithms are well suited for problems where the relationship between the input and output is roughly linear.
Overall, Inductive bias is a fundamental aspect of machine learning and understanding it is important for selecting the appropriate algorithm for a given problem and tuning its parameters to achieve the best possible performance.
here are a few examples of inductive bias in machine learning:
Decision Trees: Decision tree algorithms have a positive inductive bias towards hierarchically organized data. This means that they make efficient splits at each node based on the features of the data, allowing them to quickly classify new data points.
Linear Regression: Linear regression algorithms have a negative inductive bias towards non-linear data. This means that they assume that the relationship between the input and output is linear, and may not be able to capture more complex relationships. For example, if we were trying to model the relationship between temperature and ice cream sales, a linear regression algorithm would only consider linear relationships such as a straight line, and not take into account non-linear relationships such as a parabolic shape.
Neural Networks: Neural networks have a positive inductive bias towards discovering complex patterns in data. They are able to learn multiple layers of representations, which can help them to find complex relationships between the input and output. However, as they have a lot of parameters, they can be prone to overfitting.
Naive Bayes: Naive Bayes algorithm have a strong independence assumption, that is, it assumes that all the features of a dataset are independent of each other. This can be a strong assumption for certain datasets, for example, in a dataset with medical records, it will assume that symptoms are independent of the disease, which is not always the case.
k-Nearest Neighbors: k-Nearest Neighbors algorithm has a positive inductive bias towards smooth decision boundaries. This means it will tend to classify new data points based on the majority class of the k nearest training examples. However, this assumption may not be valid for certain types of data, such as data with multiple clusters or non-uniform class distributions.
It is important to note that all machine learning algorithms have some form of inductive bias, and the choice of algorithm and its corresponding bias should be chosen based on the nature of the problem and the characteristics of the data.
Inductive inference is the process of using observations to infer general rules or principles. In the context of decision trees, inductive inference is used to construct a decision tree from a set of training data. The process begins by selecting a feature or attribute from the training data and using it as the root node of the tree. The tree is then grown by recursively partitioning the data into subsets based on the values of the selected feature, and creating child nodes for each unique value. This process is repeated for each child node, using a different feature at each level of the tree, until the tree is fully grown. The result is a decision tree that can be used to make predictions about new data by traversing the tree from the root to a leaf node, following the path determined by the values of the features at each level.
Decision trees are a popular method for classification and regression tasks in machine learning. They are a type of predictive model that can be used to map input data (also known as features or attributes) to a target output (such as a class label or a numeric value).
In the case of inductive decision tree learning, the process of constructing a decision tree starts with selecting a feature from the training data as the root node, which is the topmost node of the tree. This feature is chosen based on its ability to best separate or discriminate the target output.
Next, the tree is grown by partitioning the data into subsets based on the values of the selected feature at the root node. Each unique value of the feature corresponds to a child node. This process is repeated for each child node by selecting the next feature that best separates the data at that node. This continues until a stopping criterion is met, such as a maximum tree depth or a minimum number of samples at a leaf node.
As the tree grows, it forms a series of internal nodes and leaf nodes. Internal nodes represent a decision point, where the tree splits the data based on the value of a feature, while leaf nodes represent the final outcome or prediction of the tree. To classify new data, we traverse the tree from the root node to a leaf node by following the path determined by the values of the features at each internal node. The class label or numeric value associated with that leaf node is the prediction made by the tree.
It's worth noting that decision trees are prone to overfitting if the tree is grown too deep. To overcome this problem, techniques such as pruning, which involves removing branches of the tree that do not add much value to the predictions, can be used to reduce the complexity of the tree.
Entropy is a measure of impurity or disorder in a set of data. In the context of decision trees, entropy is used to determine the best feature to split the data on at each step in the tree-building process.
A decision tree is a flowchart-like tree structure, where an internal node represents feature(or attribute), the branch represents a decision rule, and each leaf node represents the outcome. The topmost node in a decision tree is known as the root node. It learns to partition the data into subsets based on the values of the input features.
The entropy of a set S of examples is defined as -∑(p(i) log2 p(i)), where p(i) is the proportion of examples in class i. The entropy is 0 if all examples in S belong to the same class, and it is maximum if the examples in S are evenly split across all classes. In decision tree learning, the goal is to construct a tree that minimizes the entropy of the target class.
At each step in building the tree, the algorithm selects the feature that results in the largest information gain, which is the difference in entropy before and after the split. The feature that results in the highest information gain is chosen as the decision node. This process is repeated on each subset of the data recursively until a stopping criterion is met, such as a maximum tree depth or a minimum number of samples in a leaf node.
In summary, entropy is a measure of impurity or disorder in a set of data and it is used to determine the best feature to split the data on at each step in the tree-building process. In decision tree learning, the goal is to construct a tree that minimizes the entropy of the target class.
Information theory is a branch of mathematics that deals with the study of the transmission, processing, and extraction of information. It was developed by Claude Shannon in the 1940s and is now widely used in fields such as communication engineering, computer science, and statistics.
A decision tree is a graphical representation of a decision-making process. It is used to model a problem and to help find the best solution by breaking it down into smaller, more manageable decisions. Each internal node represents a test on an attribute, each branch represents the outcome of the test, and each leaf node represents a class label.
Information theory can be used in the construction of decision trees in several ways. One of the main applications is in the selection of the attribute to test at each internal node. This is typically done by using measures such as information gain or gain ratio, which are based on the concept of entropy, a key concept in information theory. Entropy measures the amount of uncertainty or randomness in a system. In the case of decision trees, it is used to measure the impurity of a set of examples, with a higher entropy indicating a higher level of impurity.
Information gain and gain ratio are used to evaluate the potential of each attribute to reduce the impurity of the set of examples. The attribute with the highest gain or gain ratio is selected to be tested at the next internal node. This process is repeated recursively until the tree is fully grown.
In summary, Information theory provides the mathematical foundation for decision tree learning algorithms by defining the concept of entropy as a measure of impurity, and information gain and gain ratio as measure of the potential of each attribute to reduce the impurity of the set of examples.
Information gain and gain ratio are two measures of the potential of each attribute to reduce the impurity of the set of examples. The attribute with the highest information gain or gain ratio is selected to be tested at the next internal node. This process is repeated recursively until the tree is fully grown.
Information gain is the difference in entropy before and after a data set is split on an attribute. The attribute with the highest information gain is chosen as the decision node. This process is repeated on each subset of the data recursively until a stopping criterion is met, such as a maximum tree depth or a minimum number of samples in a leaf node.
Gain ratio is similar to information gain, but it is normalized by the entropy of the attribute. This is done to avoid selecting attributes with a large number of possible values, which would result in a high information gain but a low gain ratio.
In summary, information gain and gain ratio are two measures of the potential of each attribute to reduce the impurity of the set of examples. The attribute with the highest information gain or gain ratio is selected to be tested at the next internal node. This process is repeated recursively until the tree is fully grown.
Decision trees are a popular machine learning technique for both classification and regression problems. They are easy to understand and interpret, and can be used to build a predictive model in a few steps. The goal of decision tree learning is to create a model that predicts the value of a target variable by learning simple decision rules inferred from the data features.
Decision tree learning is a supervised machine learning technique for both classification and regression problems. It is used to build a predictive model in a few steps. The goal of decision tree learning is to create a model that predicts the value of a target variable by learning simple decision rules inferred from the data features.
A decision tree is a flowchart-like tree structure, where an internal node represents feature(or attribute), the branch represents a decision rule, and each leaf node represents the outcome. The topmost node in a decision tree is known as the root node. It learns to partition the data into subsets based on the values of the input features.
The entropy of a set S of examples is defined as -∑(p(i) log2 p(i)), where p(i) is the proportion of examples in class i. The entropy is 0 if all examples in S belong to the same class, and it is maximum if the examples in S are evenly split across all classes. In decision tree learning, the goal is to construct a tree that minimizes the entropy of the target class.
At each step in building the tree, the algorithm selects the feature that results in the largest information gain, which is the difference in entropy before and after the split. The feature that results in the highest information gain is chosen as the decision node. This process is repeated on each subset of the data recursively until a stopping criterion is met, such as a maximum tree depth or a minimum number of samples in a leaf node.
In summary, decision tree learning is a supervised machine learning technique for both classification and regression problems. It is used to build a predictive model in a few steps. The goal of decision tree learning is to create a model that predicts the value of a target variable by learning simple decision rules inferred from the data features.
Information gain is the difference in entropy before and after a data set is split on an attribute. The attribute with the highest information gain is chosen as the decision node. This process is repeated on each subset of the data recursively until a stopping criterion is met, such as a maximum tree depth or a minimum number of samples in a leaf node.
In summary, information gain is the difference in entropy before and after a data set is split on an attribute. The attribute with the highest information gain is chosen as the decision node. This process is repeated on each subset of the data recursively until a stopping criterion is met, such as a maximum tree depth or a minimum number of samples in a leaf node.
The ID3 algorithm starts with the original dataset and selects the attribute with the highest information gain as the root node of the decision tree. Information gain is a measure of the reduction in entropy (or impurity) achieved by partitioning the data based on a particular attribute. The attribute with the highest information gain is considered the most informative attribute, as it provides the most discriminatory power for differentiating between the classes.
Once the root node is selected, the data is partitioned into subsets based on the value of the root attribute. The ID3 algorithm is then recursively applied to each subset to find the next best attribute for each partition. This process continues until a stopping condition is met, such as when all the data belongs to the same class or when there are no more attributes to split on.
The ID3 algorithm is a simple and easy-to-understand algorithm for building decision trees. However, it has some limitations such as overfitting, bias towards attributes with more categories, and handling missing data.
Pruning is one of the way to overcome overfitting issue, ID3 algorithm also can be improved with more advance algorithm such as C4.5 and C5.0 which handle some of its limitation.
ID3 is a popular algorithm for constructing decision trees. It is an iterative algorithm that constructs a decision tree by recursively partitioning the data into subsets based on the values of the input features. The algorithm begins by selecting the feature that best separates the target class, and uses it as the root node of the tree. It then partitions the data into subsets based on the values of the selected feature, and creates child nodes for each unique value. This process is repeated for each child node, using a different feature at each level of the tree, until the tree is fully grown. The result is a decision tree that can be used to make predictions about new data by traversing the tree from the root to a leaf node, following the path determined by the values of the features at each level.
The ID3 algorithm is a greedy algorithm, meaning that it makes the best decision at each step without considering the future consequences of that decision. This can lead to overfitting, where the tree is grown too deep and does not generalize well to new data. To overcome this problem, techniques such as pruning, which involves removing branches of the tree that do not add much value to the predictions, can be used to reduce the complexity of the tree.
In summary, ID3 is a popular algorithm for constructing decision trees. It is an iterative algorithm that constructs a decision tree by recursively partitioning the data into subsets based on the values of the input features. The algorithm begins by selecting the feature that best separates the target class, and uses it as the root node of the tree. It then partitions the data into subsets based on the values of the selected feature, and creates child nodes for each unique value. This process is repeated for each child node, using a different feature at each level of the tree, until the tree is fully grown. The result is a decision tree that can be used to make predictions about new data by traversing the tree from the root to a leaf node, following the path determined by the values of the features at each level.
Overfitting: Decision trees can easily overfit the training data if the tree is grown too deep, leading to poor performance on unseen data.
Instability: Small changes in the data can result in a completely different decision tree. This can make the model highly sensitive to minor fluctuations in the training data.
Bias towards attributes with more levels: Decision trees are more likely to split on attributes with more levels or categories, leading to a bias towards those attributes.
Limited use for continuous variables: Decision trees are not well-suited for handling continuous variables and require them to be discretized prior to building the tree.
Unbalanced class problem: Decision tree learning can be biased towards the majority class, making it difficult to handle imbalanced datasets.
Handling missing values: Decision tree algorithms may have difficulty handling missing values, and the results can be affected by how missing values are handled.
Not good for linear relationships: Decision tree is not good for the case where the data has linear relationship.
Instance-based learning, also known as memory-based learning, is a type of supervised learning that involves storing instances or examples of the training data in memory and using them as a basis for making predictions. The basic idea behind this approach is to find the most similar instances in the training data to a new input and use them to predict the output.
The main advantage of instance-based learning is that it can handle non-linear and complex relationships between inputs and outputs, as it does not rely on a specific functional form or model structure. This makes it a good choice for problems where the underlying relationship is not well understood or where the data is noisy or non-linear.
There are two main types of instance-based learning algorithms: nearest neighbor and kernel-based.
Nearest neighbor: This algorithm finds the "k" closest instances in the training data to a new input and uses the output of these instances to make a prediction. The most common form of this algorithm is the k-nearest neighbor (k-NN) algorithm, which finds the k closest instances to the new input and assigns the most common output among them as the prediction.
Kernel-based: This algorithm uses a kernel function to find the similarity between instances. The kernel function maps the inputs to a high-dimensional feature space where the similarity is calculated. Common kernel-based algorithms include the support vector machine (SVM) and radial basis function (RBF) network.
Instance-based learning is also computationally efficient and requires very little storage space, as it only needs to store the training instances. However, it can be sensitive to the choice of distance metric and the value of k, and it can be affected by the presence of irrelevant or redundant features in the data.
The main disadvantage of instance-based learning is that it can be slow when making predictions on a large dataset, as it requires searching through all the stored instances to find the most similar ones. Additionally, it is not suitable for online learning, as it requires retraining on the entire dataset whenever new instances are added.
k-Nearest Neighbour Learning is a type of instance-based learning algorithm that uses a distance metric to find the k closest instances in the training data to a new input and uses their outputs to make a prediction. The most common form of this algorithm is the k-nearest neighbor (k-NN) algorithm, which finds the k closest instances to the new input and assigns the most common output among them as the prediction.
The k-NN algorithm is a simple and easy-to-understand algorithm that can be used for both classification and regression problems. It is a non-parametric algorithm, meaning that it does not make any assumptions about the underlying data distribution. This makes it a good choice for problems where the underlying relationship is not well understood or where the data is noisy or non-linear.
The k-NN algorithm is also computationally efficient and requires very little storage space, as it only needs to store the training instances. However, it can be slow when making predictions on a large dataset, as it requires searching through all the stored instances to find the most similar ones. Additionally, it is not suitable for online learning, as it requires retraining on the entire dataset whenever new instances are added.
The k-NN algorithm is a type of instance-based learning algorithm that uses a distance metric to find the k closest instances in the training data to a new input and uses their outputs to make a prediction. The most common form of this algorithm is the k-nearest neighbor (k-NN) algorithm, which finds the k closest instances to the new input and assigns the most common output among them as the prediction.
Locally Weighted Regression (LWR) is a technique used for non-parametric regression, which means that it does not make any assumptions about the functional form of the relationship between the input and output variables. The main idea behind LWR is to weight the data points in the vicinity of the input point of interest more heavily than the data points that are farther away. This weighting is done by assigning a weight to each data point based on its distance to the input point, with the weight decreasing as the distance increases.
The most common way to assign these weights is to use a kernel function, such as a Gaussian function, which assigns higher weights to data points that are closer to the input point and lower weights to data points that are farther away. The kernel function is defined by a parameter called the bandwidth, which controls the width of the kernel and, therefore, the size of the region of influence around the input point.
The LWR algorithm can be divided into two main steps:
For a given input point, compute the weights for each data point using the kernel function and the bandwidth. Fit a linear regression model to the weighted data, where the weights are used as the observation's importance. LWR can be used for both one-dimensional and multidimensional input data. In one-dimensional case, it is also known as "loess" (locally weighted scatterplot smoothing) and in multidimensional case it is known as "Lowess" (locally weighted scatterplot smoothing)
One of the main advantages of LWR is that it can be used to model non-linear relationships between the input and output variables. Additionally, it is more flexible than traditional linear regression models because it does not require any assumptions about the functional form of the relationship between the input and output variables. However, it can be sensitive to the choice of bandwidth and kernel function, so some trial and error may be required to find the best settings for a particular dataset.
In summary, LWR is a technique used for non-parametric regression that assigns weights to data points based on their distance to the input point of interest, with the goal of modeling non-linear relationships between the input and output variables. It is a flexible and powerful technique, but it can be sensitive to the choice of bandwidth and kernel function.
Locally Weighted Regression (LWR) is like asking your friends for help with a math problem. When you're trying to figure out what the answer is, you'll ask the friends who are closest to you first because they probably know the answer better. And the friends who are farther away, you'll ask them last because they might not know the answer as well.
In LWR, we have a lot of numbers, called data points, and we want to find out what the answer is for a new number, called an input point. Just like asking your friends, we look at the data points that are closest to the input point first and give them more importance, and we look at the data points that are farther away last and give them less importance. We use something called a "kernel" to decide how close or far away the data points are from the input point. The kernel is like a magic circle that helps us decide which friends to ask first.
Once we've asked the most important data points, we use something called "linear regression" to figure out what the answer is for the input point. And that's how LWR works, it's like asking your friends for help but instead of people, we're asking numbers.
Radial basis function (RBF) networks are a type of neural network that are used for supervised learning tasks, such as classification and regression. They are based on the concept of radial basis functions, which are functions that have a radial symmetry around a central point. In RBF networks, these functions are used as the activation functions for the neurons in the network.
RBF networks consist of two layers: an input layer and a hidden layer. The input layer receives the input data and passes it on to the hidden layer, which contains a set of neurons that are each associated with a radial basis function. Each neuron in the hidden layer computes the output of its associated radial basis function for the input data, and then passes this output to the output layer.
The output layer of an RBF network is typically a linear layer, which combines the outputs of the hidden layer neurons to produce the final output of the network. The weights of the output layer are typically determined using a method called least squares, which minimizes the difference between the network's output and the target output.
One of the main advantages of RBF networks is that they are able to approximate any continuous function, as long as the hidden layer contains enough neurons. This makes them well-suited for tasks where the underlying function is complex and non-linear. Additionally, RBF networks are relatively easy to train, as the weights of the output layer can be determined using simple linear algebra techniques.
However, there are also some disadvantages of RBF networks. One of the main issues is that the number of neurons required in the hidden layer can be quite large, which can make the network difficult to train and may lead to overfitting. Additionally, the choice of radial basis functions can also be a limiting factor, as different types of functions may be better suited for different tasks.
Overall, radial basis function networks are a powerful and versatile type of neural network that are well-suited for a wide range of supervised learning tasks. They are particularly useful for tasks where the underlying function is complex and non-linear, and they are relatively easy to train. However, they can also be difficult to train and may lead to overfitting if the number of hidden layer neurons is too large.
Radial basis function networks are like a big brain that helps computers learn new things. Just like how our brain has different parts that do different things, RBF networks have different layers that do different things too.
The first layer is called the input layer and it's where the computer gets all the information it needs to learn. Then it sends that information to the second layer, which is called the hidden layer. The hidden layer has special helpers called neurons, and each neuron has a special job. They each use something called a radial basis function to help make sense of the information they received.
The last layer is called the output layer, it takes the information from the hidden layer and makes a final decision. The final decision is what the computer thinks the right answer is. It's like when you're trying to guess what's inside a present and you use different clues to make a guess.
RBF networks are really good at learning new things, even if the thing they're learning is really hard to understand. But sometimes, if there are too many helpers in the hidden layer, the computer might get confused and make a mistake. That's why it's important to have just the right number of helpers.
Case-based learning is a teaching method that utilizes real-life scenarios or case studies as a way to teach students. It is a problem-based learning approach that encourages students to think critically and apply their knowledge to real-world situations.
The main idea behind case-based learning is that students can better understand and retain information when they are able to see how it is applied in real-life scenarios. This approach is particularly useful for subjects such as business, law, and medicine, where students must be able to apply their knowledge in practical situations.
In a case-based learning environment, students are presented with a case study or scenario and are asked to analyze and solve the problem presented. They are encouraged to use their critical thinking skills and apply their knowledge to come up with a solution. The process of analyzing and solving the case helps students to better understand the subject matter and retain the information.
One of the key benefits of case-based learning is that it allows students to see how their knowledge can be applied in the real world. This can help them to understand the relevance of the subject matter and make it more interesting to them. Additionally, it allows students to develop problem-solving skills and critical thinking skills, which are valuable in a wide range of careers.
Case-based learning is also a collaborative approach, where students work in groups to analyze and solve the case. This allows students to learn from each other and gain different perspectives on the problem. It also helps to develop teamwork and communication skills.
In conclusion, case-based learning is an effective teaching method that utilizes real-life scenarios to teach students. It helps students to understand and retain information better, and develops critical thinking and problem-solving skills. Additionally, it is a collaborative approach that allows students to learn from each other and gain different perspectives.
Case-based learning is when we learn by looking at real stories or problems that people have had. Imagine if you had a toy that was broken, and you had to figure out how to fix it. That's kind of like what we do in case-based learning. We look at a problem and try to figure out how to solve it. It's like playing detective and trying to find the answer. It's fun and helps us think better!
Artificial Neural Networks (ANNs) are a type of machine learning algorithm that are modeled after the human brain. They consist of layers of interconnected nodes, called neurons, that are designed to process information and make predictions based on that information. Artificial Neural Networks (ANNs) are a type of machine learning model inspired by the structure and function of the human brain. They consist of layers of interconnected "neurons," which process and transmit information. The connections between neurons, as well as the neurons themselves, can be adjusted, or "trained," to improve the performance of the network on a given task.
There are several types of ANNs, including feedforward neural networks, recurrent neural networks, and convolutional neural networks. Feedforward neural networks consist of layers of interconnected neurons, with the data flowing through the network in only one direction, from input to output. Recurrent neural networks, on the other hand, include connections that loop back from later layers to earlier layers, allowing the network to retain and process information over time. Convolutional neural networks are specialized for image and video recognition tasks and use convolutional layers to scan the input image and extract features of the image.
ANNs are widely used in a variety of applications such as image recognition, speech recognition, natural language processing and many more. They are also used in various industries such as finance, healthcare, and transportation.
However, ANNs can be computationally expensive to train and can require a large amount of data. They also can be prone to overfitting, which occurs when the network performs well on the training data but poorly on new, unseen data. To mitigate these issues, regularization techniques, such as dropout and weight decay, are often employed during training.
ANNs are capable of modeling non-linear relationships between input and output variables, which makes them suitable for complex problems.
ANNs can handle missing data by using a technique called backpropagation, which propagates the error from the output layer to the input layer and adjusts the weights of the connections between the neurons accordingly.
ANNs are robust to outliers and noise in the data, which makes them suitable for problems that involve noisy data.
ANNs can be used for both classification and regression problems, as well as for supervised and unsupervised learning tasks.
ANNs can be scaled up to handle large datasets and complex problems.
ANNs are computationally expensive to train, which makes them unsuitable for problems that require real-time predictions.
ANNs are prone to overfitting, which occurs when the network performs well on the training data but poorly on new, unseen data.
ANNs are difficult to interpret, which makes them unsuitable for problems that require human interpretation.
ANNs can take a long time to train, which makes them unsuitable for problems that require real-time predictions.
ANNs are not very good at generalizing to new, unseen data, which makes them unsuitable for problems that require predictions on new data.
ANNs are not very robust to noise and outliers in the data, which makes them unsuitable for problems that involve noisy data.
ANNs are not very flexible, which makes them unsuitable for problems that require a lot of flexibility.
ANNs cannot be scaled up to handle large datasets and complex problems.
Feedforward neural networks are a type of artificial neural network that are used for supervised learning tasks. They consist of layers of interconnected neurons, with the data flowing through the network in only one direction, from input to output. The neurons in the input layer receive the input data, which is then processed by the neurons in the hidden layers. The output of the neurons in the hidden layers is then passed through an activation function, which produces the output of the network.
The training process of a feedforward neural network is based on a supervised learning algorithm known as backpropagation. This algorithm adjusts the weights of the connections between the neurons based on the error between the network's predictions and the actual output. The weights are updated using a gradient descent algorithm, which helps the network learn from the training data and improve its accuracy over time.
One of the main advantages of feedforward neural networks is their simplicity, which makes them easy to understand and implement. They are also useful for supervised learning tasks, such as image recognition and spam detection. However, feedforward neural networks have some limitations, such as the inability to model non-linear relationships, and the inability to solve multi-class classification problems.
In summary, feedforward neural networks are a type of artificial neural network that are used for supervised learning tasks. They consist of layers of interconnected neurons, with the data flowing through the network in only one direction, from input to output. The training process of a feedforward neural network is based on a supervised learning algorithm known as backpropagation, which adjusts the weights of the connections between the neurons based on the error between the network's predictions and the actual output. Feedforward neural networks are simple to understand and implement, but they have some limitations such as the inability to model non-linear relationships, and the inability to solve multi-class classification problems.
Recurrent neural networks are a type of artificial neural network that are used for sequential data problems. They consist of layers of interconnected neurons, with the data flowing through the network in both directions, from input to output and from output to input. The neurons in the input layer receive the input data, which is then processed by the neurons in the hidden layers. The output of the neurons in the hidden layers is then passed through an activation function, which produces the output of the network.
The training process of a recurrent neural network is based on a supervised learning algorithm known as backpropagation. This algorithm adjusts the weights of the connections between the neurons based on the error between the network's predictions and the actual output. The weights are updated using a gradient descent algorithm, which helps the network learn from the training data and improve its accuracy over time.
One of the main advantages of recurrent neural networks is their ability to model sequential data, which makes them suitable for problems such as speech recognition and machine translation. However, recurrent neural networks have some limitations, such as the inability to model non-linear relationships, and the inability to solve multi-class classification problems.
In summary, recurrent neural networks are a type of artificial neural network that are used for sequential data problems. They consist of layers of interconnected neurons, with the data flowing through the network in both directions, from input to output and from output to input. The training process of a recurrent neural network is based on a supervised learning algorithm known as backpropagation, which adjusts the weights of the connections between the neurons based on the error between the network's predictions and the actual output. Recurrent neural networks are suitable for problems such as speech recognition and machine translation, but they have some limitations such as the inability to model non-linear relationships, and the inability to solve multi-class classification problems.
Convolutional neural networks are a type of artificial neural network that are used for image recognition problems. They consist of layers of interconnected neurons, with the data flowing through the network in only one direction, from input to output. The neurons in the input layer receive the input data, which is then processed by the neurons in the hidden layers. The output of the neurons in the hidden layers is then passed through an activation function, which produces the output of the network.
The training process of a convolutional neural network is based on a supervised learning algorithm known as backpropagation. This algorithm adjusts the weights of the connections between the neurons based on the error between the network's predictions and the actual output. The weights are updated using a gradient descent algorithm, which helps the network learn from the training data and improve its accuracy over time.
One of the main advantages of convolutional neural networks is their ability to model image data, which makes them suitable for problems such as image recognition and object detection. However, convolutional neural networks have some limitations, such as the inability to model non-linear relationships, and the inability to solve multi-class classification problems.
In summary, convolutional neural networks are a type of artificial neural network that are used for image recognition problems. They consist of layers of interconnected neurons, with the data flowing through the network in only one direction, from input to output. The training process of a convolutional neural network is based on a supervised learning algorithm known as backpropagation, which adjusts the weights of the connections between the neurons based on the error between the network's predictions and the actual output. Convolutional neural networks are suitable for problems such as image recognition and object detection, but they have some limitations such as the inability to model non-linear relationships, and the inability to solve multi-class classification problems.
Perceptron is a type of artificial neural network that is used for binary classification problems. It is a simple model that consists of a single layer of artificial neurons, also known as perceptrons. The perceptrons take in input data and produce an output, which is used to classify the input into one of two categories.
A perceptron receives input data through its input layer, which is then processed by the perceptrons in the hidden layer. The output of the perceptrons in the hidden layer is then passed through an activation function, which produces a binary output indicating the class to which the input data belongs.
The training process of a perceptron is based on a supervised learning algorithm known as the perceptron learning rule. This algorithm adjusts the weights of the perceptron's connections based on the error between the perceptron's predictions and the actual output. The weights are updated using a gradient descent algorithm, which helps the perceptron learn from the training data and improve its accuracy over time.
One of the main advantages of perceptrons is their simplicity, which makes them easy to understand and implement. They are also useful for binary classification problems, such as image recognition and spam detection. However, perceptrons have some limitations, such as the inability to model non-linear relationships, and the inability to solve multi-class classification problems.
In summary, Perceptron is a type of artificial neural network that is used for binary classification problems. It consists of a single layer of artificial neurons, which process input data and produce a binary output indicating the class to which the input data belongs. The training process of a perceptron is based on a supervised learning algorithm known as the perceptron learning rule, which adjusts the weights of the perceptron's connections based on the error between the perceptron's predictions and the actual output. Perceptrons are simple to understand and implement, but they have some limitations such as the inability to model non-linear relationships, and the inability to solve multi-class classification problems.
A Multi-Layer Perceptron (MLP) is a type of artificial neural network that is composed of multiple layers of interconnected "neurons," which process and transmit information. It is called Multi-Layer because it consists of more than one layer of neurons, typically an input layer, one or more hidden layers, and an output layer.
The input layer receives the input data and passes it to the first hidden layer. Each hidden layer receives the output from the previous layer and applies a non-linear transformation to the data before passing it to the next layer. The final output layer produces the network's output. The number of layers and the number of neurons in each layer determine the complexity of the network.
MLP's are commonly used for supervised learning tasks, such as classification and regression. They are particularly useful when the relationship between inputs and outputs is non-linear. The weights of the connections between neurons, as well as the neurons themselves, can be adjusted, or "trained," to improve the performance of the network on a given task. This is done by minimizing the difference between the network's output and the desired output, through an optimization algorithm such as backpropagation.
MLP's are a powerful tool for solving a wide range of problems, such as image recognition, speech recognition, and natural language processing. However, they can be computationally expensive to train and require a large amount of data. They also can be prone to overfitting, which occurs when the network performs well on the training data but poorly on new, unseen data. To mitigate these issues, regularization techniques, such as dropout and weight decay, are often employed during training.
MLP's are able to handle non-linear relationships between inputs and outputs, which makes them suitable for a wide range of problems.
MLP's are highly flexible and can be used for a variety of tasks, such as classification, regression, and clustering.
MLP's can be easily scaled up or down depending on the size of the problem.
MLP's are able to learn from data and adjust their weights accordingly.
MLP's can be prone to overfitting, which can lead to poor generalization performance.
MLP's can be slow to train, especially when the number of layers and neurons is increased.
MLP's can be difficult to interpret, as the weights and connections between neurons are not easily understood.
MLP's can be expensive to train, as they require a large amount of data and computing power.
Gradient descent is an optimization algorithm that is used to find the values of parameters (such as weights and biases) that minimize a loss function. The loss function measures the difference between the predicted output and the actual output, and the goal of the optimization is to find the set of parameters that minimize this difference.
In the case of a neural network, the parameters are the weights and biases of the connections between the neurons, and the loss function measures the difference between the network's output and the desired output. The gradient descent algorithm starts with initial values for the parameters and iteratively updates them in the direction of the negative gradient of the loss function with respect to the parameters, until a minimum is found.
The gradient descent algorithm has different variations like Stochastic Gradient Descent(SGD), Mini-batch Gradient Descent and Batch Gradient Descent. In the Batch Gradient Descent, the gradient is calculated on the whole dataset, and the parameters are updated after each iteration. In the Stochastic Gradient Descent, the gradient is calculated for each example in the dataset, and the parameters are updated after each example. In Mini-batch Gradient Descent, the gradient is calculated for a subset of the dataset, usually with a size of 32-512.
Gradient descent is a widely used optimization algorithm for training neural networks because it is relatively simple to implement and can handle non-linear optimization problems. However, it can be sensitive to the choice of the learning rate and the initialization of the parameters. It also can be prone to getting stuck in local minima, rather than finding the global minimum of the loss function. To mitigate these issues, several variations of the gradient descent algorithm have been developed, such as Momentum, Adagrad, Adadelta, RMSprop and Adam which are designed to improve the stability and convergence of the optimization process.
The Delta rule, also known as the Widrow-Hoff rule, is a learning algorithm used to train artificial neural networks, particularly single-layer perceptrons. It is a variant of gradient descent algorithm. The following are the key points about the Delta rule:
The delta rule is used to adjust the weights of the connections between the neurons in a single-layer perceptron in order to minimize the difference between the predicted output and the actual output.
The delta rule uses the gradient of the error function with respect to the weights to determine the direction and amount of weight updates.
The weight updates are proportional to the negative gradient of the error function, with a learning rate parameter controlling the magnitude of the updates.
The delta rule works by calculating the error between the network's output and the desired output and then adjusting the weights to reduce the error.
The delta rule is able to learn linear decision boundaries, but it is not suitable for non-linear decision boundaries.
It is sensitive to the choice of the learning rate and the initialization of the weights
It can be prone to getting stuck in local minima, rather than finding the global minimum of the error function.
The delta rule is computationally efficient and easy to implement, making it a popular choice for training single-layer perceptrons.
The delta rule is a widely used algorithm for online learning, where the weights are updated after each input-output pair.
The delta rule is a special case of the more general backpropagation algorithm, which is used to train multi-layer perceptrons.
The Delta rule, also known as the Widrow-Hoff rule, is a learning algorithm used to train artificial neural networks, particularly single-layer perceptrons. It is a variant of gradient descent algorithm which is used to adjust the weights of the connections between the neurons in a single-layer perceptron in order to minimize the difference between the predicted output and the actual output.
The delta rule uses the gradient of the error function with respect to the weights to determine the direction and amount of weight updates. The error function is typically the mean squared error between the predicted and actual output. The gradient is computed using the chain rule and backpropagation algorithm. The weight updates are proportional to the negative gradient of the error function, with a learning rate parameter controlling the magnitude of the updates.
The delta rule works by calculating the error between the network's output and the desired output, and then adjusting the weights to reduce the error. The delta rule updates the weights incrementally, after each input-output pair, which makes it particularly suitable for online learning. The delta rule is able to learn linear decision boundaries, but it is not suitable for non-linear decision boundaries.
It is sensitive to the choice of the learning rate and the initialization of the weights. If the learning rate is too large, the network may overshoot the minimum of the error function, while if it is too small, the network may converge too slowly. The initialization of the weights can also have a large impact on the training process.
The delta rule is computationally efficient and easy to implement, making it a popular choice for training single-layer perceptrons. However, it can be prone to getting stuck in local minima, rather than finding the global minimum of the error function. To mitigate this issue, several variations of the delta rule have been developed, such as the Levenberg-Marquardt algorithm, which uses a combination of gradient descent and the Gauss-Newton method to improve the stability and convergence of the optimization process.
The delta rule is a special case of the more general backpropagation algorithm, which is used to train multi-layer perceptrons. Backpropagation algorithm is an extension of the delta rule, which uses the chain rule of calculus to compute the gradients of the error function with respect to the weights. It allows the weights to be updated simultaneously, rather than incrementally, which can improve the convergence rate of the optimization process.
A Multi-Layer Network (MLN) is a type of artificial neural network that is composed of multiple layers of interconnected "neurons," which process and transmit information. It is called Multi-Layer because it consists of more than one layer of neurons, typically an input layer, one or more hidden layers, and an output layer.
The input layer receives the input data and passes it to the first hidden layer. Each hidden layer receives the output from the previous layer and applies a non-linear transformation to the data before passing it to the next layer. The final output layer produces the network's output. The number of layers and the number of neurons in each layer determine the complexity of the network.
In contrast to single-layer perceptrons, which are only capable of solving linear problems, multi-layer networks, also called multi-layer perceptrons (MLP) are able to solve non-linear problems. The additional layers allow the network to learn more complex representations of the input data and can improve the performance of the network on a given task.
MLN's are commonly used for supervised learning tasks, such as classification and regression. They are particularly useful when the relationship between inputs and outputs is non-linear. The weights of the connections between neurons, as well as the neurons themselves, can be adjusted, or "trained," to improve the performance of the network on a given task. This is done by minimizing the difference between the network's output and the desired output, through an optimization algorithm such as backpropagation.
MLN's are a powerful tool for solving a wide range of problems, such as image recognition, speech recognition, and natural language processing. They are also used in various industries such as finance, healthcare, and transportation. However, they can be computationally expensive to train and require a large amount of data. They also can be prone to overfitting, which occurs when the network performs well on the training data but poorly on new, unseen data. To mitigate these issues, regularization techniques, such as dropout and weight decay, are often employed during training.
Backpropagation is a supervised learning algorithm used to train artificial neural networks, particularly multi-layer perceptrons. It is used to calculate the gradient of the error function with respect to the weights of the network, and to update the weights in the direction of the negative gradient. The algorithm is based on the chain rule of calculus, which allows the gradient to be calculated efficiently by passing error back through the network.
The Backpropagation algorithm consists of two phases: the forward phase and the backward phase. In the forward phase, the input is passed through the network to produce an output, and the error is calculated by comparing the output to the desired output. In the backward phase, the error is propagated back through the network to calculate the gradient of the error function with respect to the weights.
The backward phase starts with the output layer, where the error is calculated as the difference between the predicted output and the actual output. The error is then propagated back through the network, layer by layer, using the chain rule of calculus. The chain rule allows the error to be decomposed into a product of the error and the derivative of the activation function. The error is then multiplied by the derivative of the activation function to calculate the error for the previous layer. This process is repeated until the error reaches the input layer, where the gradient of the error function with respect to the weights can be calculated.
The gradient of the error function with respect to the weights is used to update the weights in the direction of the negative gradient. The weights are updated by subtracting the product of the learning rate and the gradient from the current weight. The learning rate is a hyperparameter that controls the magnitude of the weight updates. The gradient is calculated using the chain rule and backpropagation algorithm. The gradient is computed by passing the error back through the network, layer by layer, using the chain rule of calculus. The chain rule allows the error to be decomposed into a product of the error and the derivative of the activation function. The error is then multiplied by the derivative of the activation function to calculate the error for the previous layer. This process is repeated until the error reaches the input layer, where the gradient of the error function with respect to the weights can be calculated.
The Backpropagation algorithm is a supervised learning algorithm used to train artificial neural networks, particularly multi-layer perceptrons. It is used to calculate the gradient of the error function with respect to the weights of the network, and to update the weights in the direction of the negative gradient. The algorithm is based on the chain rule of calculus, which allows the gradient to be calculated efficiently by passing error back through the network.
The Backpropagation algorithm consists of two phases: the forward phase and the backward phase. In the forward phase, the input is passed through the network to produce an output, and the error is calculated by comparing the output to the desired output. In the backward phase, the error is propagated back through the network to calculate the gradient of the error function with respect to the weights.
The backward phase starts with the output layer, where the error is calculated as the difference between the predicted output and the actual output. The error is then propagated back through the network, layer by layer, using the chain rule of calculus. The chain rule allows the error to be decomposed into a product of the error at the current layer and the derivative of the activation function at the current layer, with respect to the input of the current layer.
The gradient of the error function with respect to the weights is then calculated by multiplying the error at the current layer with the input of the previous layer. The weights are then updated in the direction of the negative gradient, with a learning rate parameter controlling the magnitude of the updates. The learning rate parameter is used to control the speed of the algorithm, the larger the learning rate the faster the algorithm will converge, but if the learning rate is too high, the algorithm might oscillate and not converge.
The Backpropagation algorithm is widely used to train multi-layer perceptrons because it is relatively simple to implement and can handle non-linear optimization problems. However, it can be sensitive to the choice of the learning rate and the initialization of the parameters. It also can be prone to getting stuck in local minima, rather than finding the global minimum of the loss function. To mitigate these issues, several variations of the Backpropagation algorithm have been developed, such as Momentum, Adagrad, Adadelta, RMSprop and Adam which are designed to improve the stability and convergence of the optimization process.
The Backpropagation algorithm is a supervised learning algorithm used to train artificial neural networks, particularly multi-layer perceptrons. It is used to calculate the gradient of the error function with respect to the weights of the network, and to update the weights in the direction of the negative gradient. The algorithm is based on the chain rule of calculus, which allows the gradient to be calculated efficiently by passing error back through the network.
The error function is typically the mean squared error between the predicted and actual output, and it is defined as:
E = 1/2 * Σ(y - t)^2
where y is the predicted output of the network, t is the target output and the sum is taken over all training examples.
The Backpropagation algorithm consists of two phases: the forward phase and the backward phase. In the forward phase, the input is passed through the network to produce an output, and the error is calculated by comparing the output to the desired output. In the backward phase, the error is propagated back through the network to calculate the gradient of the error function with respect to the weights.
The backward phase starts with the output layer, where the error is calculated as the difference between the predicted output and the actual output. The error term for the output layer is defined as:
δ = (y - t) * f'(net)
where net is the weighted input to the output neuron, f'(net) is the derivative of the activation function with respect to net and t is the target output.
The error term is then propagated back through the network, layer by layer, using the chain rule of calculus. The chain rule allows the error to be decomposed into a product of the error at the current layer and the derivative of the activation function at the current layer, with respect to the input of the current layer.
The gradient of the error function with respect to the weights is then calculated by multiplying the error at the current layer with the input of the previous layer. The weights are then updated in the direction of the negative gradient, with a learning rate parameter controlling the magnitude of the updates.
The weight updates for a particular layer are given by:
w(t+1) = w(t) - η δ x
where w(t) is the weight at time step t, η is the learning rate, δ is the error term and x is the input to the neuron.
The backpropagation algorithm is then applied iteratively, updating the weights after each input-output pair until the error function converges to a minimum.
In summary, the Backpropagation algorithm is a supervised learning algorithm used to train multi-layer perceptrons by minimizing the error function using gradient descent. The algorithm is based on the chain rule of calculus and it consists of two phases: the forward phase, where the input is passed through the network to produce an output and the error is calculated and the backward phase, where the error is propagated back through the network to calculate the gradient of the error function with respect to the weights, which are updated in the direction of the negative gradient.
The Backpropagation algorithm is a supervised learning algorithm used to train artificial neural networks, particularly multi-layer perceptrons. It is used to calculate the gradient of the error function with respect to the weights of the network, and to update the weights in the direction of the negative gradient. The algorithm is based on the chain rule of calculus, which allows the gradient to be calculated efficiently by passing error back through the network.
The error function is typically the mean squared error between the predicted and actual output, and it is defined as:
E = 1/2 * Σ(y - t)^2
where y is the predicted output of the network, t is the target output and the sum is taken over all training examples. The error function measures the difference between the predicted output and the actual output, and the goal of the Backpropagation algorithm is to find the set of weights that minimize this difference.
The Backpropagation algorithm consists of two phases: the forward phase and the backward phase. In the forward phase, the input is passed through the network to produce an output, and the error is calculated by comparing the output to the desired output. In the backward phase, the error is propagated back through the network to calculate the gradient of the error function with respect to the weights.
The forward phase starts by passing the input data through the input layer of the network, which consists of a set of neurons that perform simple computations such as weighting and summing the input data. The output of the input layer is then passed to the next layer, called the hidden layer, which applies a non-linear transformation to the data before passing it to the next layer. The hidden layer(s) typically use an activation function such as sigmoid, ReLU, or tanh to introduce non-linearity in the network, allowing it to learn complex representations of the input data. The final output layer produces the network's output.
The backward phase starts with the output layer, where the error is calculated as the difference between the predicted output and the actual output. The error term for the output layer is defined as:
δ = (y - t) * f'(net)
where net is the weighted input to the output neuron, f'(net) is the derivative of the activation function with respect to net and t is the target output.
The error term is then propagated back through the network, layer by layer, using the chain rule of calculus. The chain rule allows the error to be decomposed into a product of the error at the current layer and the derivative of the activation function at
Okay, so imagine you have a big toy box full of different toys, and you want to teach your robot friend how to put the toys away in the right spot. But the robot doesn't know where each toy goes yet, so you have to show it.
So first, you show the robot a toy and tell it where it goes, like "this toy goes in the blue box." The robot tries to put the toy away, but it might not always get it right the first time. So you check and tell it if it's correct or not. This is like the forward phase of the Backpropagation algorithm, where the input is passed through the network and the error is calculated by comparing the output to the desired output.
Then, after you've shown the robot a few toys and it's made a few mistakes, you help the robot understand where it went wrong. You say "Oh, you put that toy in the red box instead of the blue box, let's try again." And you keep helping the robot until it gets it right. This is the backward phase of the Backpropagation algorithm, where the error is propagated back through the network to calculate the gradient of the error function with respect to the weights, and the weights are updated in the direction of the negative gradient.
So, this way the robot learn where each toy goes and how to put them away correctly. And eventually, the robot will be able to put the toys away all by itself!
Backpropagation is a supervised learning algorithm that is used to train artificial neural networks, particularly multi-layer perceptrons. It is used to adjust the weights of the connections between neurons in the network, in order to minimize the difference between the predicted output and the actual output.
In simple words, backpropagation is a method of training neural networks by adjusting the weights of the connections between neurons in order to minimize the error between predicted and actual output.
The algorithm consists of two main steps. The first step, called the forward pass, is where the input is passed through the network, and the output is generated. The second step, called the backward pass, is where the error is calculated and propagated back through the network to adjust the weights.
The backpropagation algorithm uses the chain rule of calculus to calculate the gradient of the error function with respect to the weights. The gradient is then used to adjust the weights in the direction of the negative gradient using an optimization algorithm like gradient descent.
It's important to note that backpropagation is sensitive to the choice of the learning rate and the initialization of the weights. If the learning rate is too large, the network may overshoot the minimum of the error function, while if it is too small, the network may converge too slowly. The initialization of the weights can also have a large impact on the training process.
Backpropagation is widely used and is considered one of the most important algorithm in deep learning and is used to train multi-layer perceptrons and it allows the network to learn complex representations of the input data and improve the performance of the network on a given task.
Generalization is the ability of a machine learning model to make accurate predictions on new, unseen data. It is a crucial aspect of any machine learning model, as the ultimate goal is to be able to make predictions on new data, rather than just on the data used to train the model.
Generalization is achieved by ensuring that the model is able to learn the underlying patterns in the data, rather than memorizing specific examples. This is done by using appropriate regularization techniques, such as dropout or weight decay, which help to prevent overfitting, which occurs when a model becomes too complex and starts to fit the noise in the data, rather than the underlying patterns.
Another important aspect of generalization is the ability to handle different types of data. A model that is trained on a specific type of data may not perform well on other types of data, even if the data is similar. This is known as overfitting to the training data or having a high variance. To address this, techniques such as cross-validation and data augmentation can be used to ensure that the model is exposed to a wide range of data during training.
In addition to regularization and handling different types of data, it's also important to have a good amount of data during the training process. As the size of the data increases, a model is able to learn more complex patterns, while still generalizing well to new data. This is why deep learning models are able to achieve state-of-the-art performance on many tasks, as they are able to learn from large amounts of data.
In summary, generalization is the ability of a machine learning model to make accurate predictions on new, unseen data. It is achieved by using appropriate regularization techniques, handling different types of data, and having a good amount of data during the training process.
Generalization is like when you learn how to do something new, like tie your shoes. At first, you might have trouble doing it, but with practice, you get better and better at it. And soon, you can tie your shoes not just on your own shoes, but on other people's shoes too, even if they are different sizes or colors. This is like a robot learning a new task, it can learn to do it not just on one set of examples but on a lot of different examples, this way it can do it on new, unseen examples too.
Unsupervised learning is like when you play with your toy cars. You can drive them around and make them do different things, but you don't have a specific plan or instructions for what you want them to do. You're just exploring and having fun with them. It's the same with unsupervised learning, the computer is given a set of data and it is free to explore and find patterns or relationship on its own, without any specific instructions or labels. It's like the computer is playing with the data, trying to figure out what it can do with it.
Self-Organizing Maps (SOM) algorithm is a type of unsupervised learning algorithm that is used to reduce the dimensionality of large datasets and visualize high-dimensional data in a low-dimensional space. SOM is particularly useful for exploring and visualizing complex, non-linear relationships in the data.
The SOM algorithm works by creating a map of neurons, where each neuron represents a point in the low-dimensional space. The neurons are organized in a grid, and the distance between neurons represents the similarity between the data points they represent.
The SOM algorithm starts by randomly initializing the weights of the neurons, and then it repeatedly updates the weights of the neurons based on the input data. During the training process, the algorithm iteratively selects a random data point and finds the neuron that is most similar to the data point. This neuron is called the "winning neuron", and its weights are updated to be more similar to the data point. The weights of the neurons that are close to the winning neuron are also updated, but to a lesser degree.
The SOM algorithm can be visualized as a map of neurons, where each neuron represents a point in the low-dimensional space. The neurons are organized in a grid, and the distance between neurons represents the similarity between the data points they represent.
SOM algorithm is particularly useful for exploring and visualizing complex, non-linear relationships in the data. It is widely used in data mining, image processing, speech recognition and natural language processing.
In summary, Self-Organizing Maps (SOM) is a type of unsupervised learning algorithm that is used to reduce the dimensionality of large datasets and visualize high-dimensional data in a low-dimensional space. It is based on a neural network architecture that consists of a grid of neurons, where each neuron represents a point in the low-dimensional space. The algorithm iteratively updates the weights of the neurons based on the input data and organizes them in a way that reflects the similarity between the data points they represent. SOM is widely used in various applications such as data mining, image processing, speech recognition and natural language processing.Self-Organizing Maps (SOM) algorithm is a type of unsupervised learning algorithm that is used to reduce the dimensionality of large datasets and visualize high-dimensional data in a low-dimensional space. SOM is particularly useful for exploring and visualizing complex, non-linear relationships in the data.
The SOM algorithm works by creating a map of neurons, where each neuron represents a point in the low-dimensional space. The neurons are organized in a grid, and the distance between neurons represents the similarity between the data points they represent.
The SOM algorithm starts by randomly initializing the weights of the neurons, and then it repeatedly updates the weights of the neurons based on the input data. During the training process, the algorithm iteratively selects a random data point and finds the neuron that is most similar to the data point. This neuron is called the "winning neuron", and its weights are updated to be more similar to the data point. The weights of the neurons that are close to the winning neuron are also updated, but to a lesser degree.
The SOM algorithm can be visualized as a map of neurons, where each neuron represents a point in the low-dimensional space. The neurons are organized in a grid, and the distance between neurons represents the similarity between the data points they represent.
SOM algorithm is particularly useful for exploring and visualizing complex, non-linear relationships in the data. It is widely used in data mining, image processing, speech recognition and natural language processing.
In summary, Self-Organizing Maps (SOM) is a type of unsupervised learning algorithm that is used to reduce the dimensionality of large datasets and visualize high-dimensional data in a low-dimensional space. It is based on a neural network architecture that consists of a grid of neurons, where each neuron represents a point in the low-dimensional space. The algorithm iteratively updates the weights of the neurons based on the input data and organizes them in a way that reflects the similarity between the data points they represent. SOM is widely used in various applications such as data mining, image processing, speech recognition and natural language processing.
SOM is like when you play with a puzzle. You have many different puzzle pieces and you have to figure out how to put them together. SOM is like a robot that helps you put the puzzle together. It takes all the pieces, and it tries to figure out which pieces go together. It starts by putting random pieces together, but as it goes along, it gets better and better at figuring out which pieces go together. Eventually, it can put the whole puzzle together and it can even show you a picture of what the puzzle looks like when it's finished. SOM is like a helper robot that helps you understand the puzzle and make sense of all the pieces.
There are various variants of the Self-Organizing Maps (SOM) algorithm that have been developed to improve its performance and adapt it to different types of data and applications. Some of the most popular variants of SOM include:
Growing SOM: This variant of SOM is used to train large datasets that cannot fit into memory. It starts with a small number of neurons and gradually increases the number of neurons as the training progresses. This allows the algorithm to handle large datasets without running out of memory.
Hierarchical SOM: This variant of SOM is used to visualize high-dimensional data in a hierarchical manner. It starts with a small number of neurons, and then adds more neurons as the training progresses. The new neurons are organized in a hierarchical manner, where the neurons at higher levels represent more general features, while the neurons at lower levels represent more specific features.
Adaptive SOM: This variant of SOM is used to adapt the algorithm to different types of data. It uses an adaptive learning rate and neighborhood function to adjust the parameters of the algorithm to the characteristics of the data. This allows the algorithm to converge faster and produce more accurate results.
Kohonen's Feature Maps: This variant of SOM is used to perform feature extraction and dimensionality reduction on the input data. It uses a special neighborhood function, called the Gaussian neighborhood function, to compute the similarity between the input data and the neurons. This allows the algorithm to preserve the local structure of the data and produce more accurate results.
Batch-SOM: This variant of SOM is used to improve the convergence of the algorithm. It updates the weights of the neurons in batches, rather than updating them one by one. This allows the algorithm to converge faster and produce more accurate results.
In summary, Self-Organizing Maps (SOM) algorithm has several variants that have been developed to improve its performance, adapt it to different types of data and applications. These variants include Growing SOM, Hierarchical SOM, Adaptive SOM, Kohonen's Feature Maps, Batch-SOM. They are used for different purposes like handling large datasets, visualizing high-dimensional data in a hierarchical manner, adapting the algorithm to different types of data, and improve the convergence of the algorithm.
There is a variant of the Self-Organizing Maps (SOM) algorithm called Growing Self-Organizing Maps (GSOM) which is also a unsupervised learning algorithm that is used to reduce the dimensionality of large datasets and visualize high-dimensional data in a low-dimensional space.
GSOM is similar to SOM, but instead of having a fixed grid of neurons, it starts with only a few neurons and it grows the number of neurons as needed. It is like when you play with building blocks, at first you have only a few blocks, but as you build more, you need more blocks to make the structure bigger.
GSOM works by starting with a small number of neurons and it repeatedly updates the weights of the neurons based on the input data. As the training process progresses, if the algorithm finds that there is a lot of data that is not well represented by the current map, it will add new neurons to the map to better represent the data.
Like SOM, GSOM is particularly useful for exploring and visualizing complex, non-linear relationships in the data and it is widely used in various applications such as data mining, image processing, speech recognition and natural language processing.
In summary, Growing Self-Organizing Maps (GSOM) is a variant of the Self-Organizing Maps (SOM) algorithm. It is an unsupervised learning algorithm that is used to reduce the dimensionality of large datasets and visualize high-dimensional data in a low-dimensional space, like SOM, but instead of having a fixed grid of neurons, it starts with only a few neurons and it grows the number of neurons as needed. GSOM is widely used in various applications such as data mining, image processing, speech recognition and natural language processing.
Deep learning is a subset of machine learning that is based on artificial neural networks. It is a method of teaching computers to learn from data and make predictions or decisions without being explicitly programmed. Deep learning algorithms use multiple layers of artificial neurons to learn and process complex patterns in data.
The key feature of deep learning is the use of multiple layers of neural networks, called layers. Each layer learns different features of the data and passes them on to the next layer. The more layers in the network, the more complex the patterns that can be learned. This is why deep learning is often referred to as "deep" neural networks.
Deep learning algorithms can be used for a wide range of applications such as image recognition, natural language processing, speech recognition, and self-driving cars. For example, in image recognition, a deep learning algorithm can be trained on a large dataset of images and their labels. It can then be used to identify objects in new images, even if they are slightly different from the images it was trained on.
Deep learning algorithms can also be used in natural language processing, where they can be trained on large datasets of text to understand the meaning of words and sentences. This can be used for tasks such as language translation, sentiment analysis, and text generation.
Deep learning algorithms can also be used in speech recognition, where they can be trained on large datasets of speech to understand the sounds and words that make up speech. This can be used for tasks such as voice recognition and voice-controlled assistants.
Deep learning algorithms can also be used in self-driving cars, where they can be trained on large datasets of images and sensor data to understand the environment and make decisions about how to drive.
Deep learning algorithms are often trained using a technique called backpropagation, which is a method of adjusting the weights of the artificial neurons based on the errors made by the network during training. This allows the network to learn and improve over time.
Deep learning is a powerful and versatile method of teaching computers to learn from data and make predictions or decisions. It has the potential to revolutionize many industries and improve our lives in many ways.
Convolutional layers are the fundamental building blocks of convolutional neural networks (CNNs). They are used to extract features from the input image and pass them on to the next layer for further processing.
A convolutional layer applies a set of filters, or kernels, to the input image. Each filter is a small matrix of weights that is used to detect a specific pattern in the image. For example, a filter may be designed to detect edges, shapes, or textures.
The convolution operation is applied to the input image and each filter, resulting in a set of feature maps. Each feature map represents the output of the filter applied to a specific region of the input image. The feature maps are then passed on to the next layer for further processing.
Convolutional layers can have multiple filters, each of which is designed to detect a different pattern in the image. This allows the CNN to extract multiple features from the image simultaneously.
The filters in a convolutional layer are typically learned during training, using a technique called backpropagation. This allows the CNN to learn and improve over time, as it is exposed to more data.
Convolutional layers can also have different parameters such as stride and padding. The stride is the number of pixels that the filter is moved each time it is applied to the image. Padding is the number of pixels added to the edges of the image to ensure that the filter is applied to all regions of the image.
Convolutional layers are essential for extracting features from images and videos in a way that is robust to changes in scale, rotation, and viewpoint. They are the foundation of CNNs and are used in a wide range of applications, including image recognition, object detection, video analysis, and self-driving cars.
An activation function is a mathematical function that is applied to the output of a neuron in an artificial neural network. Its purpose is to introduce non-linearity into the output of the neuron, allowing the neural network to learn and model more complex patterns in the data.
Activation functions are typically applied element-wise to the output of a neuron, meaning that each element in the output is transformed by the function. The most common activation functions used in neural networks are the sigmoid function, the rectified linear unit (ReLU) function, and the hyperbolic tangent (tanh) function.
The sigmoid function is a smooth function that maps any input value to a value between 0 and 1. This function is often used in the output layer of a neural network when the output represents a probability.
The ReLU function is a piecewise linear function that maps any input value less than 0 to 0 and any input value greater than or equal to 0 to the input value. This function is often used in the hidden layers of a neural network because it is computationally efficient and helps to reduce the vanishing gradient problem.
The tanh function is a smooth function that maps any input value to a value between -1 and 1. This function is similar to the sigmoid function but maps to a wider range of values. It is often used in the hidden layers of a neural network.
Activation functions are used in neural networks to introduce non-linearity, allowing the network to learn and model more complex patterns in the data. They are an essential component of neural networks and are used in a wide range of applications, including image recognition, natural language processing, and speech recognition.
In addition to these three activation functions, researchers have proposed other types of activation function such as Leaky ReLU, Parametric ReLU and Exponential Linear Unit (ELU). Each one of them has its own advantages and disadvantages, and the choice of activation function depends on the context of the problem and the network architecture.
Pooling is a technique used in convolutional neural networks (CNNs) to reduce the dimensionality of the feature maps produced by the convolutional layers. It is used to reduce the spatial size of the feature maps and to allow the network to learn more abstract features from the data.
The most common types of pooling used in CNNs are max pooling and average pooling. Max pooling selects the maximum value from a set of adjacent pixels in the feature map and assigns it to the corresponding location in the pooled feature map. Average pooling, on the other hand, calculates the average value from a set of adjacent pixels and assigns it to the corresponding location in the pooled feature map.
Pooling is typically applied to the feature maps with a small window, called pooling window or kernel, that is moved over the feature map. The size of the window is typically 2x2 or 3x3, and the stride is usually set to the same value as the window size. This results in a reduction of the spatial size of the feature maps by a factor of 2 or 3.
Pooling is typically applied after one or more convolutional layers, and it helps to reduce the dimensionality of the feature maps and to make the network more robust to small changes in the input image. This is because pooling is able to remove the small variations in the feature maps and keep only the most important features.
Pooling also helps to reduce overfitting, as it reduces the number of parameters in the network and makes the features more robust to small changes in the input image. Furthermore, it allows the network to learn more abstract features, as it is able to detect the presence of certain features, regardless of their location in the input image.
In summary, pooling is a technique used in CNNs to reduce the dimensionality of the feature maps and to make the network more robust to small changes in the input image. It helps to reduce overfitting and allows the network to learn more abstract features. It is typically applied after one or more convolutional layers and is an essential component of CNNs.
An activation function layer is a type of layer in an artificial neural network that applies an activation function to the input. The activation function is a mathematical function that is used to introduce non-linearity into the output of the neuron, allowing the neural network to learn and model more complex patterns in the data.
Activation function layer is applied after the linear combination of the input, weights and bias in a neural network. The output of the activation function layer is then passed on to the next layer in the network.
Activation function layer is an important component of neural networks, as it allows the network to learn non-linear relationships between the inputs and outputs. This is essential for modeling complex systems, such as image recognition or natural language processing.
The most common types of activation functions used in activation function layers are the sigmoid function, the rectified linear unit (ReLU) function, and the hyperbolic tangent (tanh) function. The choice of activation function depends on the context of the problem and the network architecture.
The sigmoid function is a smooth function that maps any input value to a value between 0 and 1. This function is often used in the output layer of a neural network when the output represents a probability.
The ReLU function is a piecewise linear function that maps any input value less than 0 to 0 and any input value greater than or equal to 0 to the input value. This function is often used in the hidden layers of a neural network because it is computationally efficient and helps to reduce the vanishing gradient problem.
The tanh function is a smooth function that maps any input value to a value between -1 and 1. This function is similar to the sigmoid function but maps to a wider range of values. It is often used in the hidden layers of a neural network.
In summary, an activation function layer is a type of layer in an artificial neural network that applies an activation function to the input. Activation function layer is an important component of neural networks, as it allows the network to learn non-linear relationships between the inputs and outputs. The choice of activation function depends on the context of the problem and the network architecture.
Imagine you are playing with a toy that has different colored blocks. Each block is like a layer in a toy house, and the blocks have different shapes, sizes and colors.
The first layer of the toy house is like a big filter that looks at all the colored blocks and picks out the blocks that look similar. For example, if the filter is looking for red blocks, it will pick out all the red blocks and put them together.
The second layer is like a smaller filter that looks at the blocks that the big filter picked out, and it separates the blocks into different groups based on their shape. So, all the square red blocks will be in one group, and all the round red blocks will be in another group.
The third layer is like a pooling layer. It takes the blocks that the second layer grouped together and makes them smaller, so they take up less space in the toy house. This helps the toy house to remember only the most important features of the blocks.
And finally, the last layer is like the brain of the toy house. It looks at all the small blocks that the pooling layer made and uses them to make a decision. For example, if the toy house sees a lot of small red square blocks, it might decide that it's looking at a red apple.
So, in a nutshell, the convolutional layers in a neural network are like different filters that look at the image, pick out certain features, group them together, and make them smaller, and finally the last layer is like the brain that makes a decision based on the features it has picked out.
Convolutional Neural Networks (CNN) are a type of neural network that is commonly used for image and video analysis. They are composed of several layers, each with a specific purpose.
The first layer of a CNN is typically a convolutional layer, which applies a set of filters to the input image. These filters are learned during training and are optimized to detect specific patterns in the image, such as edges, shapes, or textures. The output of the convolutional layer is a set of feature maps, which are then passed through one or more additional layers.
The next layer in a CNN is typically a pooling layer, which is used to reduce the dimensionality of the feature maps. The pooling layer applies a pooling operation, such as max pooling or average pooling, to the feature maps. This operation reduces the size of the feature maps and helps to reduce overfitting.
The final layer in a CNN is typically a fully connected layer, which is used to make a prediction or decision based on the feature maps. The fully connected layer applies a set of weights to the feature maps and produces a final output, such as a label or a probability.
Convolutional layers are the fundamental building blocks of CNNs and are used to extract features from the input image. They are followed by pooling layers that are used to reduce the dimensionality of the feature maps and make the network more robust to small changes in the input image. Finally, fully connected layers are used to make a prediction or decision based on the feature maps.
The choice of the number of layers, the architecture of the layers and the activation functions used in each layer can greatly affect the performance of the CNN, and it's important to select the right combination that fits the problem at hand.
A fully connected layer, also known as a dense layer, is a type of layer in an artificial neural network that connects all the neurons in one layer to all the neurons in the next layer. This means that each neuron in the fully connected layer receives input from all the neurons in the previous layer and sends output to all the neurons in the next layer.
Fully connected layers are typically used in the final stages of a neural network, where they make predictions or decisions based on the input data. They are also known as the output layer, and the number of neurons in this layer is usually equal to the number of output classes in the problem.
The neurons in a fully connected layer have a set of weights and a bias term that are used to compute the output of the neuron. These weights and bias terms are learned during training and are used to make predictions or decisions based on the input data.
Fully connected layers are used in a wide range of applications, including image recognition, natural language processing, and speech recognition. They are particularly useful in multi-class classification problems, where the network needs to make a prediction or decision based on multiple output classes.
In addition, fully connected layers can be stacked to create deep neural networks. These layers contain a large number of parameters and need a lot of data to be trained, this can lead to overfitting if the number of parameters is larger than the amount of data available. To solve this, regularization techniques such as dropout and L2 regularization can be used to prevent overfitting.
In conclusion, fully connected layers are a type of layer in an artificial neural network that connects all the neurons in one layer to all the neurons in the next layer. They are typically used in the final stages of a neural network, where they make predictions or decisions based on the input data. Fully connected layers are useful in multi-class classification problems and can be stacked to create deep neural networks.
The concept of convolution is a mathematical operation that is used in convolutional neural networks (CNNs) to extract features from the input data. It is a process of combining two functions to produce a third function, and it is used to combine the input data with a set of filters or kernels to extract features from the data.
There are two main types of convolution: 1D convolution and 2D convolution.
1D convolution is used for processing one-dimensional data, such as time series data, audio signals, and text data. In 1D convolution, the input data is a one-dimensional array, and the filters are also one-dimensional arrays. The convolution operation is applied to the input data and each filter, resulting in a set of feature maps. Each feature map represents the output of the filter applied to a specific region of the input data.
2D convolution is used for processing two-dimensional data, such as images and videos. In 2D convolution, the input data is a two-dimensional array, and the filters are also two-dimensional arrays. The convolution operation is applied to the input data and each filter, resulting in a set of feature maps. Each feature map represents the output of the filter applied to a specific region of the input data.
The convolution operation is a mathematical operation that is used to combine the input data with a set of filters or kernels to extract features from the data. The filters are learned during training and are optimized to detect specific patterns in the input data.
In summary, convolution is a mathematical operation used in CNNs to extract features from the input data. There are two main types of convolution: 1D convolution for processing one-dimensional data, and 2D convolution for processing two-dimensional data. The filters are learned during training and are optimized to detect specific patterns in the input data, and this process is repeated in multiple layers to extract more complex features.
Training a convolutional neural network (CNN) involves adjusting the weights and biases of the neurons in the network so that it can accurately classify or predict the output based on the input data.
The process starts by providing the network with a set of labeled training data, where the input data and its corresponding output label are known. For example, in an image classification problem, the input data would be an image, and the output label would be the corresponding class of the image (e.g. cat, dog, etc.).
The network then makes a prediction based on the input data and compares it to the correct output label. The difference between the prediction and the correct output label is then used to calculate the error or loss of the network.
The error is then propagated back through the network using a technique called backpropagation. This technique adjusts the weights and biases of the neurons in the network to reduce the error and improve the accuracy of the network.
The process of providing the network with input data, making a prediction, calculating the error, and adjusting the weights and biases is repeated multiple times with different sets of training data. This is known as an epoch. The training process continues for a certain number of epochs or until the error reaches a satisfactory level.
After training, the network is tested with a set of test data to evaluate its performance. If the network performs well on the test data, it can be deployed for real-world applications.
In summary, training a CNN involves providing the network with labeled training data, making predictions, calculating the error, and adjusting the weights and biases of the neurons in the network to reduce the error and improve the accuracy of the network. The process is repeated multiple times with different sets of training data, and the network is tested with a set of test data to evaluate its performance.
One application of convolutional neural networks is in the diagnosis of Diabetic Retinopathy (DR). DR is a common complication of diabetes and can lead to blindness if not detected and treated early. CNNs have been used to detect DR from retinal images, by analyzing the features of the image and classifying them as normal or abnormal.
In a study conducted by researchers from the University of Iowa, a convolutional neural network was used to detect DR from retinal images with an accuracy of 99.4%. The results of this study demonstrate the potential of CNNs to accurately diagnose DR from retinal images.
The researchers also noted that the accuracy of the model could be further improved by including additional data such as blood glucose levels and patient age. This indicates that CNNs could be used in the future to develop a fully automated system for diagnosing DR from retinal images.
Overall, this case study demonstrates the potential of convolutional neural networks in the diagnosis of diabetic retinopathy from retinal images.
One example of how convolutional neural networks (CNNs) can be used to build smart speakers is through natural language processing (NLP). With NLP, the speaker can understand spoken language and respond in an appropriate way. For example, a user could ask the speaker to play a certain song or provide the latest news. By using a CNN to recognize and interpret speech, the speaker can provide an accurate response. This technology could also be used to detect voice commands and activate certain features, such as a light switch or a thermostat. In addition, CNNs can be used to improve the accuracy of speech recognition, which could make it easier to use the speaker in noisy environments. In the future, CNNs could be used to create more advanced speakers that can understand complex commands and respond accordingly.
This case study has demonstrated the power of convolutional neural networks, and the potential for their use in the development of self-driving cars. The ability to accurately identify objects and interpret the environment with high accuracy and speed has been demonstrated, and could have a significant impact on the development of autonomous driving systems in the future. The use of convolutional neural networks in self-driving cars could help to reduce the number of accidents and increase the efficiency of decision-making processes, and could have a major impact on the safety and reliability of self-driving cars in the future.
Reinforcement Learning (RL) is a type of machine learning in which an agent learns to make decisions by interacting with its environment in order to maximize a reward signal. In RL, an agent learns to take actions in an environment in order to maximize a cumulative reward over time. RL algorithms use trial-and-error method to learn from past experiences and adjust their behavior accordingly to improve their performance. RL has been applied to a wide range of problems such as game playing, robotics, and decision making under uncertainty. Some popular RL algorithms include Q-learning, SARSA and actor-critic methods.
Reinforcement Learning (RL) is a type of machine learning that focuses on training agents to make decisions in an environment in order to maximize a cumulative reward signal. The goal of RL is to learn a policy, which is a mapping from states to actions, that will allow the agent to achieve the highest possible cumulative reward over time.
In RL, the agent interacts with its environment in a sequence of time steps. At each time step, the agent observes the current state of the environment and selects an action to perform. The environment then transitions to a new state and the agent receives a reward signal, which provides feedback on the quality of the action it has taken. The agent's goal is to learn a policy that will maximize the cumulative reward over time.
One of the key elements of RL is the concept of value, which refers to the expected long-term reward of being in a particular state or taking a particular action. RL algorithms use value estimates to guide the agent's decision making process. There are two main types of value estimates: action-value estimates and state-value estimates.
Action-value estimates, such as Q-learning, estimate the expected long-term reward of taking a particular action in a particular state and following the current policy thereafter. State-value estimates, such as SARSA, estimate the expected long-term reward of being in a particular state and following the current policy thereafter.
Another important concept in RL is the idea of exploration vs. exploitation. In order to learn an optimal policy, the agent must explore the environment to gather information about different states and actions. At the same time, it must also exploit the knowledge it has acquired to make decisions that will maximize its reward. There are various ways to balance exploration and exploitation, such as epsilon-greedy, boltzmann exploration, and Thompson sampling.
RL has been successfully applied to a wide range of problems, such as game playing, robotics, and decision making under uncertainty. Some popular RL algorithms include Q-learning, SARSA, actor-critic methods, and deep RL algorithms such as DQN, A3C and PPO. RL is also used in combination with other machine learning techniques, such as supervised learning and unsupervised learning, in Multi-Agent Reinforcement Learning and Inverse RL.
Overall, Reinforcement Learning is a powerful and versatile machine learning technique that has the potential to solve a wide range of problems involving decision making and control. The field is actively being researched and new advancements and algorithms are being developed to improve the performance and applicability of RL.
A learning task in Reinforcement Learning (RL) refers to the specific problem that the agent is trying to solve. This can include tasks such as playing a game, controlling a robot, or making decisions in an uncertain environment.
In general, a RL learning task can be defined as a tuple of (S, A, R, γ), where S is the set of states, A is the set of actions, R is the reward function, and γ is the discount factor.
The set of states, S, represents the different possible situations that the agent can find itself in. This can include the current position of a robot, the status of different game pieces, or the current market conditions.
The set of actions, A, represents the different actions that the agent can take in each state. This can include moving a robot, making a move in a game, or buying or selling a stock.
The reward function, R, assigns a scalar value to each state-action pair and represents the immediate reward that the agent receives for taking a particular action in a particular state. The reward function is used to guide the agent's learning and decision making process.
The discount factor, γ, is a scalar value between 0 and 1 that is used to balance the importance of immediate rewards and long-term rewards. A high discount factor places more importance on immediate rewards, while a low discount factor places more importance on long-term rewards.
The main goal of RL is to find an optimal policy, which is a mapping from states to actions, that maximizes the expected cumulative reward over time. This can be formulated as the problem of finding the policy that maximizes the expected cumulative reward given by the sum of all rewards received by the agent under the policy:
π* = argmaxπ ∑(t=0)∞ γ^tR(s_t,a_t)
The learning task in RL is to find the optimal policy, π* that maximizes this expected cumulative reward, by using the environment's feedback in the form of rewards and transitions between states.
In summary, a learning task in RL is defined by the set of states, actions, the reward function, and the discount factor and the main goal is to find an optimal policy that maximizes the expected cumulative reward over time.
One example of Reinforcement Learning (RL) in practice is the use of RL to train game-playing agents. One of the most famous examples of this is the AlphaGo program developed by Google DeepMind, which used RL to train a machine to play the board game Go at a superhuman level.
In the case of AlphaGo, the states of the game were represented by the positions of the stones on the Go board. The actions were the legal moves that could be made at each state. The reward function was designed to give a positive reward for winning a game and a negative reward for losing a game.
The RL algorithm used by AlphaGo was a variant of Q-learning, called Deep Q-Network (DQN). The DQN algorithm uses a deep neural network to approximate the action-value function, which estimates the expected long-term reward of taking a particular action in a particular state and following the current policy thereafter.
The AlphaGo program was trained using a combination of supervised learning and reinforcement learning. The supervised learning component was used to train the neural network on a dataset of expert Go games, and the RL component was used to fine-tune the network by playing against itself and learning from the results.
The training process for AlphaGo involved playing millions of games of Go against itself, gradually improving its understanding of the game and its ability to make strategic decisions. Once it had been trained, the AlphaGo program was able to beat some of the best human players in the world.
This example of AlphaGo shows how RL can be used to train agents to perform complex tasks, such as playing board games at a superhuman level, by using trial-and-error to learn from past experiences and adjust its behavior accordingly.
Another example of Reinforcement Learning (RL) in practice is the use of RL in robotics. RL can be used to train robots to perform various tasks such as grasping objects, navigating through environments, and following a specific trajectory.
One example of RL applied to robotics is a robotic arm that uses RL to learn to reach and grasp objects. In this case, the states of the system can be defined as the positions and velocities of the joints of the robotic arm, and the actions can be defined as the torques applied to the joints. The reward function could be designed such that the robot receives a high reward for successfully grasping an object and a low reward for dropping it.
RL algorithms such as Q-learning and SARSA can be used to train the robotic arm to learn a policy that maps states to actions in order to maximize the cumulative reward. The robot can learn to adjust its actions over time by trial and error and improve its grasping capabilities.
Another example is the use of RL in self-driving cars. RL can be used to train self-driving cars to make decisions such as when to accelerate, brake, or turn. In this case, the states can be defined as the current position and velocity of the car, the positions and velocities of other cars on the road, and the actions can be defined as the acceleration and steering commands. The reward function could be designed to give a high reward for successfully completing a trip and a low reward for getting into an accident.
RL algorithms can be used to train the self-driving car to learn a policy that maps states to actions in order to maximize the cumulative reward. The car can learn to adjust its actions over time by trial and error and improve its decision making capabilities.
These are just a few examples of how RL can be applied in practice to train agents to perform a wide range of tasks such as game playing, robotics and self-driving cars. There are many other examples of RL being used in various fields such as finance, energy management, healthcare, and more.
Reinforcement learning (RL) is a type of machine learning in which an agent learns to make decisions by interacting with its environment and receiving feedback in the form of rewards or punishments. There are a variety of different learning models used in RL, including:
Q-learning: One of the most popular RL models, Q-learning is a model-free algorithm that learns the optimal action-value function for a given Markov decision process (MDP).
SARSA: Another model-free algorithm, SARSA stands for "state-action-reward-state-action" and is similar to Q-learning, but it uses the expected value of the next action rather than the optimal action.
Monte Carlo: Monte Carlo methods are a class of RL algorithms that use simulations to estimate the value of a policy or action.
Policy gradient: Policy gradient methods are a class of RL algorithms that directly optimize the policy (i.e., the mapping from states to actions) rather than the value function.
Actor-Critic: Actor-Critic is a combination of both value-based and policy-based methods. Actor learns the policy and Critic learns the value function.
All these models have their own advantages and disadvantages and they are used based on the problem's requirement.
A Markov decision process (MDP) is a mathematical framework for modeling decision-making problems in which an agent interacts with an environment over a series of discrete time steps. An MDP is defined by a set of states, a set of actions, and a set of probabilities that govern the transitions between states. The key property of an MDP is that the probability of transitioning from one state to another is dependent only on the current state and the action taken, and not on any prior history. This property is known as the Markov property.
In an MDP, the agent observes the current state of the environment, selects an action based on a policy, and receives a numerical reward or penalty for the action taken. The agent's goal is to learn a policy that maximizes the expected cumulative reward over time.
The MDP consists of the following components:
State set S: The set of all possible states of the environment.
Action set A: The set of all possible actions that the agent can take in each state.
Transition function T(s, a, s'): The probability of transitioning from state s to state s' after taking action a.
Reward function R(s, a, s'): The reward or penalty associated with transitioning from state s to state s' after taking action a.
Initial state distribution π(s): The probability of starting in each state.
Discount factor γ: A value between 0 and 1 that determines the relative importance of short-term and long-term rewards.
MDPs are widely used in various fields such as control systems, operations research, artificial intelligence, and economics. They provide a mathematical foundation for modeling and solving decision-making problems that involve uncertainty, and they have been applied to a wide range of problems, including robotics, game playing, and finance.
In summary, Markov Decision Process (MDP) is a mathematical framework that provides a way to model decision-making problems under uncertainty. It helps to find the best policy that maximizes the cumulative reward over time by considering the current state, available actions and the reward obtained after taking an action. MDPs are widely used in many fields and they provide a powerful tool to model and solve decision-making problems that involve uncertainty.
Q-learning is a type of model-free reinforcement learning algorithm that is used to learn the optimal action-value function for a given Markov decision process (MDP). The goal of Q-learning is to find the best action to take in each state, in order to maximize the expected cumulative reward over time.
The Q-learning algorithm uses a Q-table to store the estimated action-values for each state-action pair. The Q-table is initialized with random values and is updated as the agent interacts with the environment. The Q-table is updated using the following update rule:
Q(s, a) = Q(s, a) + α(r + γ * max(Q(s', a')) - Q(s, a))
Where:
s is the current state a is the current action s' is the next state a' is the next action r is the reward received for taking action a in state s α is the learning rate, which determines the extent to which the new information overrides the old information γ is the discount factor, which determines the importance of future rewards The Q-table is updated after each action-reward transition in the environment. The update rule is based on the temporal difference (TD) error, which is the difference between the expected future reward and the current estimate of the action-value. The update rule adjusts the Q-value for the current state-action pair towards the expected future reward, with the learning rate determining the size of the update.
The Q-learning algorithm also uses an exploration-exploitation strategy, in which the agent explores new states and actions, while also exploiting the knowledge it has already acquired. This is done by selecting actions with a probability determined by an exploration policy, such as epsilon-greedy, which balances exploration and exploitation.
In summary, Q-learning is a model-free reinforcement learning algorithm that learns the optimal action-value function for a given Markov decision process. It uses a Q-table to store the estimated action-values for each state-action pair, and updates the Q-table using the temporal difference error. The algorithm also uses an exploration-exploitation strategy to balance exploration and exploitation.
Q-learning is a way for a computer to learn how to make good choices in a game or problem. Imagine you are playing a game where you can move around and collect treats. Each time you make a move, you get some treats. The goal is to collect as many treats as possible.
Q-learning is a way for the computer to learn the best way to move and collect treats. The computer keeps track of all the different moves it can make and how many treats it gets each time. After trying different moves, the computer will start to remember which moves are better and which ones are not so good.
The computer will then use this information to make better choices and collect more treats. Eventually, the computer will be so good at the game that it will be able to collect the most treats possible!
That's Q-learning in a nutshell, it's a way for the computer to learn what is the best choice to make by trying different options and keeping track of the reward it gets.
Q-learning is like a treasure map for a computer. Imagine the computer is trying to find treasure in a big maze. It starts at the beginning of the maze and it tries different paths to see where the treasure is. Every time it finds some treasure, it makes a note on its treasure map.
The computer's treasure map is called a Q-table. It has all the different paths the computer can take and how much treasure it found on each path. As the computer keeps exploring the maze, it starts to understand which paths have more treasure and which paths have less.
So next time, the computer can choose the path which it knows has more treasure, instead of trying a new path which might not have any treasure at all. And the computer keeps updating its treasure map as it explores more of the maze.
Eventually, the computer will have a complete treasure map and it will always know the best path to take to find the most treasure!
So, Q-learning is a way for a computer to learn the best path to take by trying different options and keeping track of the rewards it gets. Like a treasure map it helps the computer to find the best path to get the most treasure.
Q-learning is a method for a computer to learn the best decisions to make in a given situation, similar to how we humans make decisions. Imagine you are trying to plan a route to a destination, but you are not familiar with the area and you don't know the best way to get there. In this situation, you would try out different routes, and based on the time it takes, the traffic, and the scenery, you would make a note of which route you prefer.
Q-learning works in a similar way, but instead of you making the decisions, the computer does it. The computer starts by trying out different options and based on the rewards it receives for each option, it makes a note of which option is better. This is similar to making a note on your map of the routes you prefer.
As the computer continues to explore and make decisions, it starts to understand which options are better and which ones are not so good. Just like you would eventually find the best route to your destination, the computer will eventually learn the best decision to make in a given situation.
The computer keeps track of all the information it learns in a table called Q-table, similar to how you would keep track of your preferred routes in a map. And just like you would update your map as you discover new roads or shortcuts, the computer updates its Q-table as it receives new information.
In summary, Q-learning is a method that helps a computer to learn the best decisions to make in a given situation, by trying different options and making a note of which option is better. It keeps track of all the information in a Q-table, similar to how we humans keep track of our preferred routes on a map and update it as we discover new information.
Q-learning is a model-free reinforcement learning algorithm that is used to learn the optimal action-value function for a given Markov decision process (MDP). The Q-learning algorithm uses a Q-table to store the estimated action-values for each state-action pair. It updates the Q-table using the following update rule:
Q(s, a) = Q(s, a) + α(r + γ * max(Q(s', a')) - Q(s, a))
Where:
s is the current state a is the current action s' is the next state a' is the next action r is the reward received for taking action a in state s α is the learning rate, which determines the extent to which the new information overrides the old information γ is the discount factor, which determines the importance of future rewards The Q-table is updated after each action-reward transition in the environment. The update rule is based on the temporal difference (TD) error, which is the difference between the expected future reward and the current estimate of the action-value.
The Q-learning algorithm also uses an exploration-exploitation strategy, in which the agent explores new states and actions, while also exploiting the knowledge it has already acquired. This is done by selecting actions with a probability determined by an exploration policy, such as epsilon-greedy, which balances exploration and exploitation.
Additionally, Q-learning algorithm is an off-policy algorithm which means that it learns the optimal action-value function independently of the current policy being followed.
In summary, Q-learning is a model-free reinforcement learning algorithm that learns the optimal action-value function for a given Markov decision process. It uses a Q-table to store the estimated action-values for each state-action pair, and updates the Q-table using the temporal difference error. The algorithm also uses an exploration-exploitation strategy to balance exploration and exploitation and it is an off-policy algorithm.
Q-learning is a type of model-free reinforcement learning algorithm that is used to learn the optimal action-value function for a given Markov decision process (MDP). The goal of Q-learning is to find the best action to take in each state, in order to maximize the expected cumulative reward over time.
The Q-learning algorithm uses a Q-table to store the estimated action-values for each state-action pair. The Q-table is initialized with random values and is updated as the agent interacts with the environment. The Q-table is updated using the following update rule:
Q(s, a) = Q(s, a) + α(r + γ * max(Q(s', a')) - Q(s, a))
Where:
s is the current state a is the current action s' is the next state a' is the next action r is the reward received for taking action a in state s α is the learning rate, which determines the extent to which the new information overrides the old information γ is the discount factor, which determines the importance of future rewards The Q-table is updated after each action-reward transition in the environment. The update rule is based on the temporal difference (TD) error, which is the difference between the expected future reward and the current estimate of the action-value. The update rule adjusts the Q-value for the current state-action pair towards the expected future reward, with the learning rate determining the size of the update.
The Q-learning algorithm also uses an exploration-exploitation strategy, in which the agent explores new states and actions, while also exploiting the knowledge it has already acquired. This is done by selecting actions with a probability determined by an exploration policy, such as epsilon-greedy, which balances exploration and exploitation.
One of the key features of Q-Learning is that it is an off-policy algorithm, which means that it learns the optimal action-value function independently of the current policy being followed. It also doesn't require a model of the environment and it can learn from the raw data.
Q-learning is widely used in various fields such as control systems, game AI, and robotics. It can be applied to both discrete and continuous state and action spaces. However, it can suffer from problems such as overfitting and divergence when the learning rate is not set correctly.
In summary, Q-learning is a model-free reinforcement learning algorithm that learns the optimal action-value function for a given Markov decision process. It uses a Q-table to store the estimated action-values for each state-action pair, and updates the Q-table using the temporal difference error. The algorithm also uses an exploration-exploitation strategy to balance exploration and exploitation. It is an off-policy algorithm and can be applied to both discrete and continuous state and action spaces.
Q-learning is like a treasure map for a computer. Imagine the computer is trying to find treasure in a big maze. It starts at the beginning of the maze and it tries different paths to see where the treasure is. Every time it finds some treasure, it makes a note on its treasure map.
The computer's treasure map is called a Q-table. It has all the different paths the computer can take and how much treasure it found on each path. As the computer keeps exploring the maze, it starts to understand which paths have more treasure and which paths have less.
So next time, the computer can choose the path which it knows has more treasure, instead of trying a new path which might not have any treasure at all. And the computer keeps updating its treasure map as it explores more of the maze.
Eventually, the computer will have a complete treasure map and it will always know the best path to take to find the most treasure!
So, Q-learning is a way for a computer to learn the best path to take by trying different options and keeping track of the rewards it gets. Like a treasure map it helps the computer to find the best path to get the most treasure.
Deep Q-learning (DQN) is a variation of Q-learning that uses deep neural networks to approximate the Q-function. It combines the power of neural networks to generalize and approximate complex functions with the stability and ability to handle high-dimensional state spaces of Q-learning.
In DQN, instead of using a Q-table to store the estimated action-values, a neural network is used to approximate the Q-function. The input to the network is the current state, and the output is the estimated action-values for all possible actions. The network is trained to predict the Q-values using a variant of the Q-learning update rule, and it uses the backpropagation algorithm to adjust the weights of the network.
One of the key features of DQN is the use of experience replay. Experience replay is a technique that allows the agent to learn from past experiences by storing them in a replay buffer and randomly sampling them to update the network. This helps to decorrelate the data and make the learning more stable.
DQN also uses a technique called target networks. In Q-learning, the Q-values are updated using the current estimates of the Q-values, which can lead to instability in the learning process. Target networks are used to overcome this problem by having a separate network to estimate the target Q-values, which are used to update the main network.
In summary, Deep Q-Learning (DQN) is a variation of Q-learning that uses a deep neural network to approximate the Q-function. It combines the power of neural networks to generalize and approximate complex functions with the stability and ability to handle high-dimensional state spaces of Q-learning. DQN uses experience replay and target networks to overcome the stability problems of Q-learning, making the learning process more stable and robust.
Reinforcement Learning (RL) is a type of machine learning that is used to train agents to make decisions in an environment. RL algorithms learn to optimize a reward function by interacting with the environment and receiving feedback in the form of rewards or penalties. RL has been applied in a variety of areas, including:
Robotics: RL algorithms can be used to train robots to perform tasks such as grasping objects, navigation, and manipulation.
Game playing: RL has been used to train agents to play games such as chess, Go, and poker at a superhuman level.
Finance: RL can be used to optimize the trading of financial instruments, such as stocks and derivatives.
Healthcare: RL can be used to optimize the treatment of patients, such as determining the most effective drug regimen for a particular patient.
Autonomous systems: RL can be used to train autonomous systems, such as self-driving cars and drones, to make safe and efficient decisions.
Natural Language Processing (NLP): RL can be used to train a dialogue agent, such as a chatbot, to respond to user inputs in a more human-like way.
Overall, RL has the potential to be applied in many different areas, and is expected to have a significant impact on various industries.
Genetic algorithms are a type of optimization algorithm that are inspired by the process of natural selection. They are commonly used in situations where the search space is large and traditional optimization techniques may not be effective.
The basic idea behind genetic algorithms is to represent solutions to a problem as a set of parameters, called a genome. These genomes are then randomly generated and evaluated according to a fitness function, which measures how well the genome solves the problem at hand.
The best genomes are then selected to create a new generation of genomes through a process called crossover. Crossover is a genetic operator that combines the genetic information of two parent genomes to create one or more offspring genomes. Another operator called mutation is also applied to introduce small random changes in the genome.
The process of selection, crossover, and mutation is repeated for multiple generations until a satisfactory solution is found or a stopping criterion is met.
Genetic algorithms have been used to solve a wide range of problems, including function optimization, machine learning, and scheduling. They are particularly useful in situations where the solution cannot be easily modeled mathematically, and an exhaustive search of the solution space is infeasible.
There are several components that make up a genetic algorithm:
Population: A population is a set of candidate solutions, also known as individuals or chromosomes, that are represented by a genome. The genome is a set of parameters that define the solution to the problem at hand.
Fitness function: The fitness function is a measure of how well a particular individual or chromosome solves the problem. The fitness function assigns a fitness value to each individual in the population, and the individuals with the highest fitness values are selected for reproduction.
Selection: Selection is the process of choosing the individuals that will be used for reproduction. The individuals with the highest fitness values are more likely to be selected, but other selection methods such as roulette wheel selection and tournament selection can also be used.
Crossover: Crossover is a genetic operator that combines the genetic information of two parent individuals to create one or more offspring individuals. Crossover is applied to the selected individuals in order to create a new generation of individuals.
Mutation: Mutation is a genetic operator that introduces small random changes in the genome of an individual. Mutation is applied to the offspring individuals to introduce genetic diversity and to prevent premature convergence.
Stopping criterion: A stopping criterion is a condition that determines when the genetic algorithm should stop. The stopping criterion can be based on the number of generations, the fitness of the best individual, or the time elapsed.
Replacement: Replacement is the process of determining which individuals from the current population will be retained for the next generation and which individuals will be replaced by the new offspring individuals.
The cycle of reproduction in a genetic algorithm typically consists of the following steps:
Initialization: The initial population of individuals is randomly generated and evaluated according to the fitness function.
Selection: The individuals in the population are selected for reproduction based on their fitness values. Individuals with higher fitness values are more likely to be selected.
Crossover: The selected individuals are combined to create new offspring individuals through the process of crossover. The genetic information of two parent individuals is combined to create one or more offspring individuals.
Mutation: The offspring individuals are then subjected to mutation, which introduces small random changes in their genomes.
Evaluation: The fitness of the new offspring individuals is evaluated according to the fitness function.
Replacement: The new offspring individuals are then incorporated into the population, and the weakest individuals are replaced.
Repeat: The process of selection, crossover, mutation, evaluation, and replacement is repeated for multiple generations until a satisfactory solution is found or the stopping criterion is met.
Termination: The genetic algorithm terminates when the stopping criterion is met and the best solution is returned.
Note that depending on the specific implementation of the GA, steps can be modified, skipped or added.
There are several types of genetic algorithms, each with its own unique characteristics and applications. Some common types of genetic algorithms include:
Steady-State Genetic Algorithm: A steady-state genetic algorithm maintains a constant population size and replaces individuals one at a time. This type of genetic algorithm is more suitable for problems with a large search space and a large number of constraints.
Generational Genetic Algorithm: A generational genetic algorithm creates a new population of individuals at each generation by selecting the best individuals from the current population, applying crossover and mutation, and then evaluating the fitness of the new individuals. This type of genetic algorithm is more suitable for problems with a small search space and few constraints.
Hybrid Genetic Algorithm: A hybrid genetic algorithm combines different components or operators from different genetic algorithms to create a new algorithm. For example, it could combine a steady-state genetic algorithm with a particle swarm optimization algorithm. This type of genetic algorithm is useful when a problem has multiple local optima.
Memetic Algorithm: A memetic algorithm is a combination of genetic algorithm and local search method. It uses genetic algorithm to explore the solution space and then applies local search method to fine-tune the solution. This type of genetic algorithm can be useful for problems where the solutions are complex and have multiple local optima.
Genetic Programming: Genetic programming uses genetic algorithms to evolve computer programs or models. It is used to generate new models or algorithms automatically, without human intervention.
Evolutionary Strategy: Evolutionary strategy is a genetic algorithm variant that uses a continuous representation of the solution and uses mutation as the only variation operator. It's used in problems where the representation in a continuous space is natural and more informative than a discrete one.
These are some examples of the types of genetic algorithms, but there are many other variations and hybrids that have been proposed.
In the context of genetic algorithms, crossover is a genetic operator that combines the genetic information of two parent individuals to create one or more offspring individuals. The process of crossover is used to create a new generation of individuals that inherits the genetic characteristics of the parent individuals.
Crossover is typically implemented by selecting a crossover point, or multiple crossover points, in the genome of the parent individuals. The genetic information on one side of the crossover point is taken from one parent individual, and the genetic information on the other side of the crossover point is taken from the other parent individual. The resulting offspring individual is a combination of the genetic information of the two parent individuals.
There are several different types of crossover operators, each with its own unique characteristics and applications. Some examples include:
Single-point crossover: A single-point crossover operator selects a single point in the genome of the parent individuals and combines the genetic information on either side of the point to create the offspring individuals.
Two-point crossover: A two-point crossover operator selects two points in the genome of the parent individuals and combines the genetic information between the points to create the offspring individuals.
Multi-point crossover: A multi-point crossover operator selects multiple points in the genome of the parent individuals and combines the genetic information between the points to create the offspring individuals.
Uniform crossover: A uniform crossover operator randomly selects individual genes or alleles from the parent individuals to create the offspring individuals.
Arithmetic crossover: A arithmetic crossover operator applies mathematical operations to combine the parents' information to create the offspring individuals.
The choice of crossover operator depends on the nature of the problem and the representation of the solution. The goal of crossover is to introduce genetic diversity and to preserve the good genetic characteristics of the parent individuals in the offspring individuals.
In the context of genetic algorithms, mutation is a genetic operator that introduces small random changes in the genome of an individual. The process of mutation is used to introduce genetic diversity and to prevent premature convergence.
Mutation is typically implemented by randomly selecting one or more genes in the genome of an individual and changing their values. The amount of change introduced by the mutation operator is usually small, to avoid introducing drastic changes to the genome.
There are several different types of mutation operators, each with its own unique characteristics and applications. Some examples include:
Bit-flip mutation: A bit-flip mutation operator flips the value of a randomly selected bit in the genome of an individual. This operator is commonly used for binary-encoded genomes.
Gaussian mutation: A Gaussian mutation operator adds a random value, drawn from a Gaussian distribution, to the value of a randomly selected gene in the genome of an individual. This operator is commonly used for continuous-valued genomes.
Non-uniform mutation: A non-uniform mutation operator applies a different probability of mutation to each gene in the genome of an individual, based on the gene's position or importance.
Swap mutation: A swap mutation operator swaps the position of two randomly selected genes in the genome of an individual.
Scramble mutation: A scramble mutation operator randomly reorders a subset of the genes in the genome of an individual.
The choice of mutation operator depends on the nature of the problem and the representation of the solution. The goal of mutation is to introduce small random changes in the genome of an individual to explore new regions of the search space and to prevent the population from getting stuck in a local optimum.
Genetic programming (GP) is a subfield of genetic algorithms (GA) where the solutions are computer programs or models, rather than a fixed set of parameters. GP uses genetic algorithms to evolve computer programs or models automatically, without human intervention.
The basic idea behind GP is to represent a computer program or a model as a tree structure, where each node in the tree represents an operator or a terminal. The leaves of the tree are the terminal nodes, which represent inputs or constants. The internal nodes represent the operators, which take one or more inputs and produce one output.
The GP process starts with a randomly generated population of tree structures, which are evaluated according to a fitness function. The fitness function measures how well the tree structure solves the problem at hand. The best trees are then selected for reproduction, and new trees are generated through the process of crossover and mutation. The process is repeated for multiple generations until a satisfactory solution is found or a stopping criterion is met.
GP has been used to solve a wide range of problems, such as function optimization, symbolic regression, image processing, and artificial intelligence. It is particularly useful in situations where the solution cannot be easily modeled mathematically, and an exhaustive search of the solution space is infeasible. GP is also used in the area of automatic programming or automatic design of algorithms.
GP has some challenges, like the complexity of the tree structures that can grow exponentially and the difficulty of finding the appropriate fitness function. Some techniques have been proposed to deal with these challenges such as tree manipulation operators, bloat control, and multiple fitness functions.
In the context of genetic algorithms, models of evolution and learning refer to the different ways in which the genetic algorithm can evolve and learn from the data.
One popular model of evolution in genetic algorithms is the Darwinian model, which is based on the principles of natural selection. In this model, individuals in the population compete for resources, and the individuals that are better adapted to the environment are more likely to survive and reproduce. This process of selection and reproduction leads to the evolution of the population over time.
Another model of evolution in genetic algorithms is the Lamarckian model, which is based on the principles of inheritance of acquired characteristics. In this model, individuals can improve their fitness during their lifetime and pass on these improvements to their offspring. This process leads to the evolution of the population over time.
Models of learning in genetic algorithms can be divided into two categories: supervised learning and unsupervised learning. In supervised learning, the genetic algorithm is provided with a set of labeled examples, and the goal is to learn a model that can generalize to new examples. In unsupervised learning, the genetic algorithm is provided with a set of unlabeled examples, and the goal is to discover the underlying structure of the data.
Genetic algorithms can also be combined with other machine learning methods to create hybrid models. For example, a genetic algorithm can be used to optimize the parameters of a neural network, or a genetic algorithm can be used to evolve a set of rules for a decision tree.
In general, the choice of the model of evolution and learning depends on the nature of the problem, the representation of the solution, and the available data. Genetic algorithms are a flexible optimization method and can be adapted to a wide range of problems and scenarios.
Genetic algorithms have been applied to a wide range of problems and fields, including but not limited to:
Function optimization: Genetic algorithms can be used to find the global minimum or maximum of a function with multiple local optima. They are particularly useful in situations where the function cannot be easily modeled mathematically.
Machine learning: Genetic algorithms can be used to optimize the parameters of a machine learning model, such as a neural network or a decision tree. They are also used to evolve the structure of a machine learning model, such as the number of layers or the number of nodes in a neural network.
Scheduling: Genetic algorithms can be used to solve scheduling problems, such as the traveling salesman problem, the job-shop scheduling problem, and the resource-constrained project scheduling problem. They are particularly useful in situations where the solution space is large and traditional optimization techniques may not be effective.
Robotics: Genetic algorithms can be used to optimize the control parameters of a robot, such as the gains of a PID controller or the weights of a neural network controller. They are also used to evolve the structure of a robot, such as the number of legs or the number of sensors.
Game playing: Genetic algorithms can be used to optimize the strategy of a game-playing agent, such as a chess-playing program or a Go-playing program. They are also used to evolve the structure of a game-playing agent, such as the number of layers or the number of nodes in a neural network.
Finance: Genetic Algorithms can be used to optimize portfolio allocations, and also to optimize trading strategies.
Engineering design: Genetic Algorithms can be used to optimize the design of engineering systems, such as antenna design, aerodynamic design, and structural design.
Medicine: Genetic Algorithms can be used to identify genetic markers associated with diseases, to predict the effectiveness of treatment, and to design new drugs.
Art and Music: Genetic Algorithms can be used to generate art and music, by evolving the parameters of a generative model or the notes of a composition.
These are some examples of the application of genetic algorithms, but they can be applied in many other fields as well, where optimization is needed and traditional optimization techniques may not be effective.